Задача 77571 ...
Условие
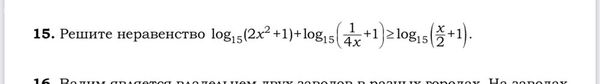
Решение
[m]\log_{15}(2x^2+1) + \log_{15}(\frac{1+4x}{4x}) ≥ \log_{15}(\frac{x+2}{2})[/m]
Область определения для функции логарифма:
{ 1/(4x) + 1 > 0
{ x/2 + 1 > 0
{ x ≠ 0
Решаем:
{ 1/(4x) > -1 U 1/(4x) > 0
{ x > -2 U x > 0
{ x ≠ 0
Получаем:
{ x < -1/4 U x > 0
{ x > -2 U x > 0
{ x ≠ 0
Область определения: x ∈ (-2; -1/4) U (0; +oo)
Сумма логарифмов равна логарифму произведения.
[m]\log_{15} (\frac{(2x^2+1)(4x+1)}{4x}) ≥ \log_{15}(\frac{x+2}{2})[/m]
Основание 15 > 1, значит, функция логарифма возрастает.
Поэтому, если один логарифм больше, то и выражение под логарифмом больше.
[m]\frac{(2x^2+1)(4x+1)}{4x} ≥ \frac{x+2}{2}[/m]
[m]\frac{(2x^2+1)(4x+1)}{4x} - \frac{x+2}{2} ≥ 0[/m]
Приводим к общему знаменателю 4x:
[m]\frac{(2x^2+1)(4x+1)}{4x} - \frac{2x(x+2)}{4x} ≥ 0[/m]
[m]\frac{8x^3+4x+2x^2+1-2x^2-4x}{4x} ≥ 0[/m]
[m]\frac{8x^3+1}{4x} ≥ 0[/m]
1) Если x ∈ (-2; -1/4), то знаменатель 4x < 0.
А так как дробь больше 0, то числитель:
8x^3 + 1 ≤ 0
x^3 ≤ -1/8
x ≤ -1/2
С учетом области определения:
x ∈ (-2; -1/2]
2) Если x ∈ (0; +oo), то знаменатель 4x > 0
А так как дробь больше или равна 0, то числитель:
8x^3 + 1 ≥ 0
Это выполнено при всех x > 0.
Ответ: x ∈ (-2; -1/2] U (0; +oo)