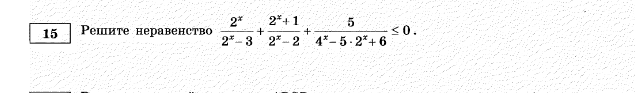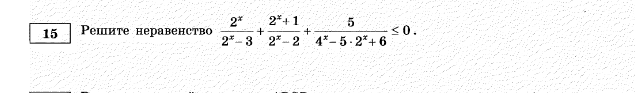Сделаем замену переменных: 2^х=t. Получим неравенство: t/(t-3)+(t+1)/(t-2)+5/(t^2-5t+6)≤0. Разложим квадратный трехчлен t^2-5t+6 на множители. Для этого решим квадратное уравнение: t^2-5t+6=0. по теореме Виета х1=2, х2=3. t^2-5t+6=(t-3)(t-2). t/(t-3)+(t+1)/(t-2)+5/(t-3)(t-2)≤0. приведем к общему знаменателю: (t^2-2t+t^2-3t+t-3+5)/(t-3)(t-2)≤0 => (2t^2-4t+2)/(t-2)(t-3)≤0 => (t^2-2t+1)/(t-2)(t-3)≤0 => (t-1)^2/(t-2)(t-3)≤0. В числителе положительное число, на знак неравенства не влияет.Знаменатель не должен равняться 0. (t-2)(t-3)≠0 => t-2≠0 и t-3≠0 => t≠2 и t≠3.
Нанесем точки на числовую прямую. Выбираем промежуток со знаком -. Ответ (2;3)