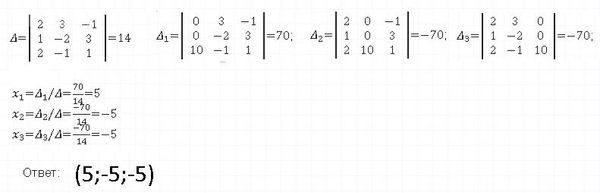Задача 77493 Найти вектор x, зная, что он...

664455c5b2c99e1bb8f6d376

5/15/2024 6:28:39 AM

Найти вектор x, зная, что он перпендикулярен к a={2; 3; –1}, b={1; –2; 3} и удовлетворяет условию x(2i–j+k)=10

5f3ea7e3faf909182968ddd9

5/15/2024 9:05:35 AM

★

vector{x}=(x_(1); x_(2);x_(3))


vector{x} перпендикулярен к vector{a}={2; 3; –1}

значит скалярное произведение векторов равно 0

Скалярное произведение векторов, заданных своими координатами

равно сумме произведений одноименных координат

2*x_(1)+3*x_(2)+(-1)*x_(3)=0



vector{x} перпендикулярен к vector{b}={1; –2; 3}}

значит скалярное произведение векторов равно 0

Скалярное произведение векторов, заданных своими координатами

равно сумме произведений одноименных координат

1*x_(1)+(-2)*x_(2)+3*x_(3)=0



vector{x} удовлетворяет условию

vector{x} *(2vector{i}–vector{j} +vector{k} )=10

скалярное произведение векторов равно 10

Скалярное произведение векторов, заданных своими координатами

равно сумме произведений одноименных координат

2*x_(1)+(-1)*x_(2)+1*x_(3)=10


Решаем систему трех уравнений с тремя неизвестными

2*x_(1)+3*x_(2)+(-1)*x_(3)=0
1*x_(1)+(-2)*x_(2)+3*x_(3)=0
2*x_(1)+(-1)*x_(2)+1*x_(3)=10

Решаем систему методом Крамера: