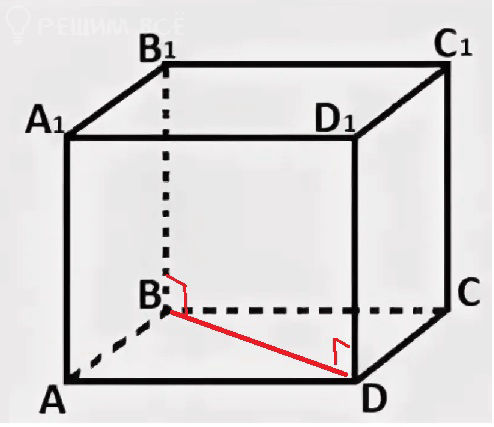
Задача 77472 в единичном кубе A...D1 найдите...

664346f07295381996cf2b37

5/14/2024 11:12:37 AM

в единичном кубе A...D1 найдите расстояние между прямыми BB1 и DD1

5f3ea7e3faf909182968ddd9

5/14/2024 11:18:57 AM

★

BB_(1) ⊥ плоскости АВСD, значит перпендикулярна любой прямой, лежащей в этой плоскости, в том числе

BB_(1) ⊥ BD

Аналогично,

СС_(1) ⊥ плоскости АВСD, значит перпендикулярна любой прямой, лежащей в этой плоскости, в том числе

СС_(1) ⊥ BD


Получили, что

BD ⊥ BB_(1)

BD ⊥ CC_(1)


BD- общий перпендикуляр к указанным прямым, значит расстояние равно длине диагонали BD

BD=sqrt(BC^2+CD^2)=sqrt(1^2+1^2)=sqrt(2)