Задача 77464 решите неравенства, с подробным...
Условие
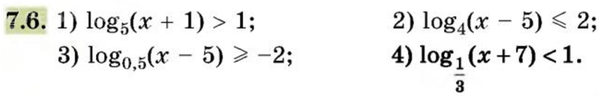
Решение
[m]log_{5}(x+1)>1[/m]
Неравенство имеет смысл при [red] [m](x+1)>0[/m][/red]
Так как
[m]1=log_{5}5[/m], то
неравенство принимает вид:
[m]log_{5}(x+1)>log_{5}5[/m]
Так как логарифмическая функция с основанием 5[i] возрастающая[/i],
значит большему значению функции соответствует большее значение аргумента
получаем неравенство:
[m](x+1)>5[/m]
С учетом [red] [m](x+1)>0[/m][/red]
решаем систему неравенств
[m]\left\{\begin {matrix}x+1>5\\x+1>0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}x>4\\x>-1\end {matrix}\right.[/m]
Решение системы:[m]x>4[/m]
О т в е т. (4;+ ∞ )
2)
[m]log_{4}(x-5) ≤2 [/m]
Неравенство имеет смысл при [red] [m](x-5)>0[/m][/red]
Так как
[m]2= log_{4}16[/m], то
неравенство принимает вид:
[m]log_{4}(x-5) ≤ log_{4}16[/m]
Так как логарифмическая функция с основанием 5[i] возрастающая[/i],
значит большему значению функции соответствует большее значение аргумента
получаем неравенство:
[m](x-5) ≤ 16[/m]
С учетом [red] [m](x-5)>0[/m][/red]
решаем систему неравенств
[m]\left\{\begin {matrix}x-5≤ 16\\x-5>0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}x ≤ 16+5\\x>5\end {matrix}\right.[/m]⇒[m]\left\{\begin {matrix}x ≤ 21\\x>5\end {matrix}\right.[/m]
Решение системы:[m]5 < x ≤21 [/m]
О т в е т. (5;21]
3)
рис. к заданию 1)