Задача 77428 Найти область сходимости ряда...
Условие
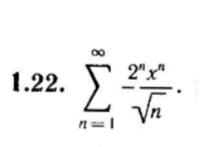
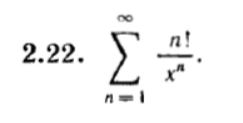
математика ВУЗ
159
Решение
★
[m]\lim \limits_{n \to \infty} \frac{a(n+1)}{a(n)}[/m]
Если этот предел < 1, то ряд сходится. Если он > 1, то ряд расходится.
1) [m]\lim \limits_{n \to \infty} \frac{2^{n+1} x^{n+1}}{\sqrt{n+1}} : \frac{2^{n} x^{n}}{\sqrt{n}} = \lim \limits_{n \to \infty} \frac{2^{n+1} x^{n+1}}{2^{n} x^{n}} \cdot \frac{\sqrt{n}}{\sqrt{n+1}} = 2x \cdot 1 = 2x < 1[/m]
x < 1/2
x ∈ (-0,5; 0,5)
2) [m]\lim \limits_{n \to \infty} \frac{(n+1)!}{x^{n+1}} : \frac{n!}{x^{n}} = \lim \limits_{n \to \infty} \frac{(n+1)!}{n!} \cdot \frac{x^{n}}{x^{n+1}} = \lim \limits_{n \to \infty} \frac{n+1}{x} = \infty[/m]
Этот ряд расходится при любых значениях x.