Задача 77421 Здравствуйте, надо решить задачу...
Условие
Провести полное исследование функции соответствии с планом исследования , данное решение не устроило преподавателя 


Решение
1.
Область определения:
x ≠ -2
D(y)=(- ∞ ;-2) U (-2;+ ∞ )
2.
Область определения не является симметричной относительно нуля.
Функция не является ни четной, ни нечетной.
Функция не является периодической
3
Нули функции
[m]x+6+\frac{9}{x+2}=0[/m]
[m]\frac{(x+6)\cdot (x+2)+9}{x+2}=0[/m]
[m]\frac{x^2+6x+2x+12+9}{x+2}=0[/m]
[m]\frac{x^2+8x+21}{x+2}=0[/m]
[m]x^2+8x+21=0[/m]
D=64-4*21 <0
Уравнение не имеет корней.
Точек пересечения с осью Ох нет
При x=0
[m]y(0)=0+6+\frac{9}{0+2}[/m]
y(0)=10,5
(0;10,5) - точка пересечения с осью Оу
4.
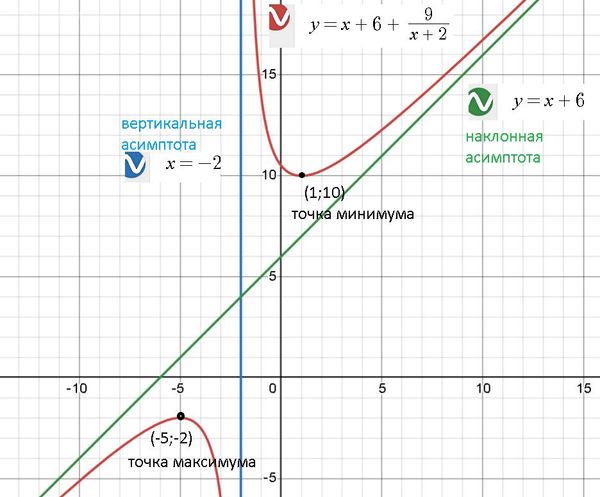
Прямая [m] x=-2 [/m] является [i] вертикальной[/i] асимптотой.
Так как [m] lim_{x → -2-0}(x+6+\frac{9}{x+2})=- ∞ [/m]
Так как [m] lim_{x → -2+0}(x+6+\frac{9}{x+2})=+∞ [/m]
[i]Горизонтальных[/i] асимптот нет , так как
[m] lim_{x → +∞}(x+6+\frac{9}{x+2})=+ ∞ [/m]
[m] lim_{x → -∞}(x+6+\frac{9}{x+2})=- ∞ [/m]
[i] Наклонная[/i] асимптота: [b][m]y=x+6[/m][/b]
так как
[m] k= lim_{x → ∞}\frac{f(x)}{x}=lim_{x → ∞}(\frac{x+6+\frac{9}{x+2}}{ x})= lim_{x → ∞}(1+\frac{6}{x}+\frac{9}{x(x+2)}=1[/m]
[m]b= lim_{x → ∞}(f(x)-kx)= lim_{x → ∞}(x+6+\frac{9}{x+2}-x)=lim_{x → ∞}(6+\frac{9}{x+2})=6+0=6[/m]
[b]Исследование с помощью первой производной[/b]:
[m]y`=(x+6+\frac{9}{x+2})`[/m]
[m]y`=1+0+9\cdot ((x+2)^{-1})`[/m]
[m]y`=1+9*(-2)*(x+2)^{-1-1}[/m]
[m]y`=1-\frac{9}{(x+2)^2}[/m]
y`=0
(x+2)^2-9=0
((x+2)-3)*(x+2+3)=0
(x-1)*(x+5)=0
x=1 или x=-5
Расставляем знак производной на области определения
____+_ (-5) ___-___ (-2) ____-_________ (1) __+___
y`>0 на (- ∞ ; 1) и на (1;+ ∞ )
Значит функция возрастает на (- ∞ ; 1) и на (1;+ ∞ )
y`<0 на (-5;-2) и на (-2;1)
Значит, функция убывает на (-5;-2) и на (-2;1)
x=-5 - точка максимума, производная меняет знак с + на -
[m]y(-5)=-5+6+\frac{9}{(-5+2)}=1-3=-2[/m]
(-5;-2) - точка максимума
x=1 - точка минимума, производная меняет знак с - на +
[m]y(1)=1+6+\frac{9}{(1+2)}=7+3=10[/m]
(1;10) - точка минимума
[b]Исследование с помощью второй производной:[/b]
[m]y``=(1-\frac{9}{(x+2)^2})`[/m]
[m]y``=(1)`-9\cdot (x+2)^{-2})`[/m]
[m]y``=0-9\cdot (-2)(x+2)^{-2-1}[/m]
[m]y``=18(x+2)^{-3}[/m]
[m]y``=\frac{18}{(x+2)^3}[/m]
y``<0 при x ∈ (- ∞ ;-2)
Значит кривая выпукла вверх ( ∩ ) на (- ∞ ;-2)
y``>0 при x ∈ (2;+ ∞)
Значит кривая выпукла вниз( ∪ ) на (- 2;+∞)