Задача 77413 ...
Условие
10.27. ∫ (√(1 + x^2) / x) dx, x = tg t.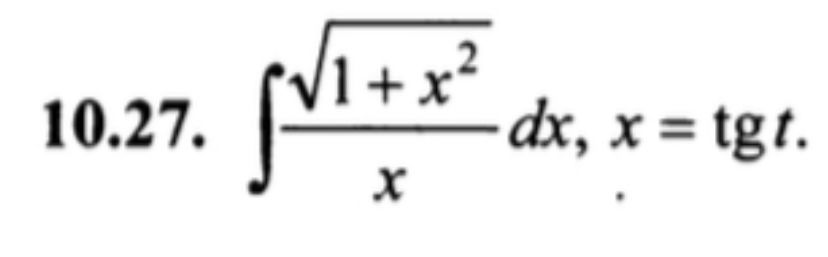
математика ВУЗ
183
Решение
★
[m]1+x^2=1+tg^2t=\frac{1}{cos^2t}[/m]
[m]\sqrt{1+x^2}=\sqrt{\frac{1}{cos^2t}}=\frac{1}{cost}[/m]
[m]dx=(tgt)`dt=\frac{1}{cos^2t}dt[/m]
тогда
[m] ∫ \frac{\sqrt{1+x^2}}{x}dx= ∫ \frac{\frac{1}{cost}}{tgt}\frac{1}{cos^2t}dt= ∫\frac{1}{sint\cdot cos^2t}dt= [/m]
Домножим и числитель и знаменатель на [m]sint[/m]
[m]=∫\frac{sint}{sin^2t\cdot cos^2t}dt=-∫\frac{d(cost)}{(1-cos^2t)\cdot cos^2t}dt=∫\frac{d(cost)}{(cos^2t-1)\cdot cos^2t}dt [/m]
Замена
[m]u=cost[/m]
