Задача 77412 ...
Условие
10.26. ∫ (x² dx) / √(1 - x²), x = sin t.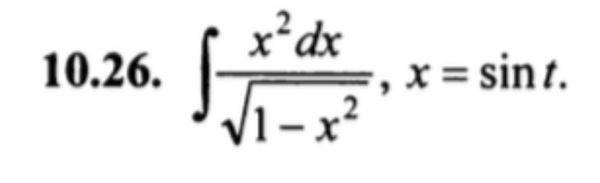
Решение
[m]1-x^2=1-sin^2t=cos^2t[/m]
[m]\sqrt{1-x^2}=\sqrt{cos^2t}=cost[/m]
[m]dx=(sint)`dt=costdt[/m]
Тогда
[m] ∫ \frac{x^2}{\sqrt{1-x^2}}dx= ∫ \frac{sin^2t}{cost}\cdot costdt= ∫ sin^2tdt= ∫ \frac{1-cos2t}{2}dt=\frac{1}{2} ∫ dt-\frac{1}{2} ∫ cos2tdt=[/m]
[m]=\frac{1}{2}t-\frac{1}{2}\cdot (\frac{1}{2}sin2t)+C=\frac{1}{2}t-\frac{1}{4}sin2t+C[/m]
===========
Обратный переход к переменной х
[m]sint = x[/m] ⇒ [m]t = arcsinx[/m]
[m]cost=\sqrt{1-x^2}[/m]
[m]sin2t=2sint\cdot cost=2\cdot x\cdot \sqrt{1-x^2}[/m]
===========
[m]=\frac{1}{2}arcsinx-\frac{1}{4}\cdot 2\cdot x\cdot \sqrt{1-x^2}+C=\frac{1}{2}arcsinx-\frac{1}{2}x\cdot \sqrt{1-x^2}+C[/m]
О т в е т.[m]\frac{1}{2}arcsinx-\frac{1}{2}x\cdot \sqrt{1-x^2}+C[/m]