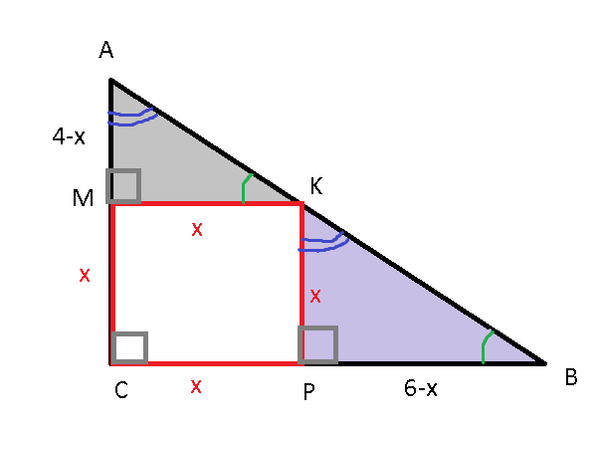
Задача 77403 В прямоугольный треугольник вписан...

6245cc109047d823797edd39

5/9/2024 5:35:21 PM

В прямоугольный треугольник вписан квадрат так, что они имеют общий прямой угол и вершины квадрата расположены на сторонах треугольника. Вычислите площадь квадрата, если катеты треугольника равны 4 см и 6 см.

5f3ea7e3faf909182968ddd9

5/10/2024 12:55:05 PM

★

Пусть сторона квадрата равна х

Δ АМК ∼ Δ КРВ по двум углам

AM:KP=MK:PB

(4-x):x=x:(6-x)

Произведение крайних членов пропорции

(4-x)*(6-x)

равно произведению средних

х*х

(4-x)*(6-x)=х*х


24-6х-4х+x^2=x^2


24=10x

x=2,4

S_(квадрата)=x^2=2,4^2=[b]5,76[/b]