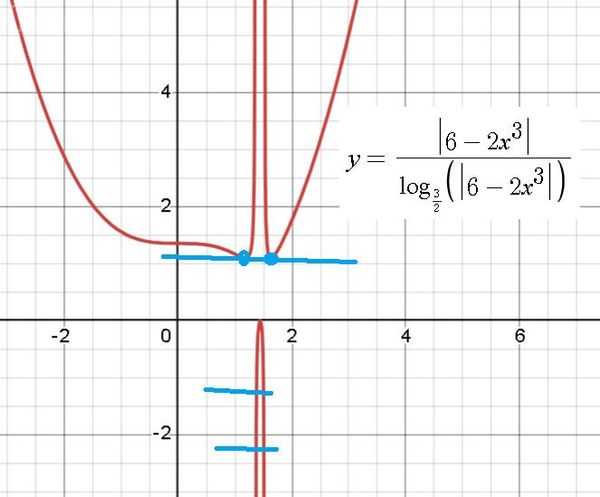
Задача 77383 При каких значениях параметра c...
Условие
Решение
|6-2x^3|=t
t>0
t ≠ 0, так как находится под знаком логарифма
Уравнение принимает вид:
t=c*log_(3/2)t
[m]c=\frac{t}{log_{\frac{3}{2}}t}[/m]
Рассматриваем функцию
[m]y=\frac{t}{log_{\frac{3}{2}}t}[/m]
log_(3/2)t ≠ 0 ⇒ [b]t ≠ 1[/b]
Находим производную
[m]y`=\frac{(t)`\cdot log_{\frac{3}{2}}t -t\cdot \frac{1}{t\cdot ln\frac{3}{2}}}{log^2_{\frac{3}{2}}t}[/m]
[m]y`=0[/m]
[m] log_{\frac{3}{2}}t - \frac{1}{\cdot ln\frac{3}{2}}=0[/m] ⇒ [m]t=e[/m]
[m]y(e)=\frac{e}{log_{\frac{3}{2}}e}[/m] ⇒ [m]y(e)=eln\frac{3}{2}[/m]
Убедитесь, что это точка максимума.
Так как t=|6-2x^2|, то будет и вторая ветвь графика в левой полуплоскости относительно оси Оу
Выбрала ответ из предложенных
(- ∞ ;0) U [m]=\frac{e}{log_{\frac{3}{2}}e}[/m]