Задача 77154 Контрольная работа. Нужно с чертежами и...
Условие
Нужно с чертежами и решением.
100 баллов
Решение
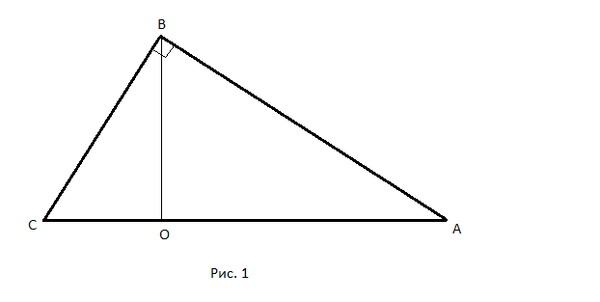
Смотрите Рис. 1.
Во-первых, вся гипотенуза
AC = CO + OA = 36 + 64 = 100 см.
Во-вторых, треугольники BCO и ABO подобны ABC, потому что они имеют одинаковые углы.
У BCO и ABC общий угол C и одинаковые прямые углы
ABC = BOC = 90°
У ABO и ABC общий угол A и одинаковые прямые углы
ABC = AOB = 90°
Поэтому их стороны пропорциональны друг другу.
Малые катеты относятся к гипотенузам:
CO : BC = BC : AC
BC^2 = CO*AC = 36*100 = 3600
BC = sqrt(3600) = 60
Большие катеты относятся к гипотенузам:
OA : AB = AB : AC
AB^2 = OA*AC = 64*100 = 6400
AB = sqrt(6400) = 80
2) В прямоугольном треугольнике ∠ B = 90°, BO - высота.
BC = 7 см, AC = 25 см.
Найти BO. AB, AO, OC.
Подходит тот же Рис. 1.
Треугольники BCO и ABO подобны ABC, потому что они имеют одинаковые углы.
По теореме Пифагора:
AB^2 = AC^2 - BC^2 = 25^2 - 7^2 = 625 - 49 = 576
AB = sqrt(576) = 24 см
Большие катеты относятся к гипотенузам:
BO : BC = AB : AC
BO = AB*BC/AC = 24*7/25 = 168/25 = 6,72 см
AO : AB = AB : AC
AO = AB^2/AC = 24^2/25 = 576/25 = 23,04 см
Малые катеты относятся к гипотенузам:
OC : BC = BC : AC
OC = BC^2/AC = 7^2/25 = 49/25 = 1,96 см
3) Гипотенуза прямоугольного треугольника равна 11 см, а синус одного из острых углов равен 0,8.
Найти длину катетов.
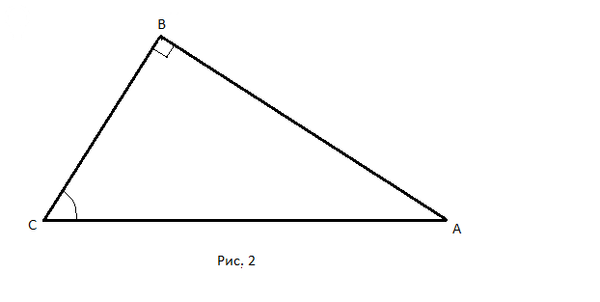
Смотрите Рис. 2.
AC = 11 см, sin C = 0,8.
Заметим, что по правилам приведения:
sin (90° - a) = cos a
Поэтому:
sin A = cos C = sqrt(1 - sin^2 C) = sqrt(1 - 0,8^2) = sqrt(1 - 0,64) = sqrt(0,36) = 0,6
Катет равен гипотенузе, умноженной на синус противолежащего угла:
BC = AC*sin A = 11*0,6 = 6,6 см
AB = AC*sin C = 11*0,8 = 8,8 см
4) Тангенс острого угла прямоугольного треугольника равен 2, а площадь треугольника равна 25 дм^2.
Найти катеты.
Подходит тот же Рис. 2.
tg C = 2, S(ABC) = 25 дм^2
Тангенс острого угла равен отношению противолежащего катета к прилежащему.
tg C = AB/BC = 2
Площадь прямоугольного треугольника равна половине произведения катетов.
S(ABC) = AB*BC/2 = 25
Получили систему уравнений. Решаем подстановкой:
AB = 2*BC
AB*BC = 2*BC*BC = 25
BC^2 = 25/2 = 12,5
BC = sqrt(12,5) = sqrt(25/2) = 5/sqrt(2) = 5sqrt(2)/2 см
AB = 2*BC = 5sqrt(2) см
5) Угол B = 90°, BO - высота треугольника ABC. AB = c, BC = a
Выразить длину отрезков AO и CO через величины a и c.
Подходит опять Рис. 1
Гипотенуза AC по теореме Пифагора:
AC = sqrt(BC^2 + AB^2) = sqrt(a^2 + c^2)
Треугольники BCO и ABO подобны ABC, потому что они имеют одинаковые углы.
Точно также, как в номере 2:
AO = AB^2/AC = c^2/sqrt(a^2 + c^2)
CO = BC^2/AC = a^2/sqrt(a^2 + c^2)