Задача 77135 Стереометрия,правильная шестиугольная...

65199db047ac953d0ca0181d

4/27/2024 2:04:40 PM

Стереометрия,правильная шестиугольная призма ABCDEFA1B1C1D1E1F1,AB=AA1=2, Нужно найти угол между прямыми BC1 и CF1

5f3ea7e3faf909182968ddd9

4/27/2024 6:07:57 PM

★

FE_(1) || BC_(1)

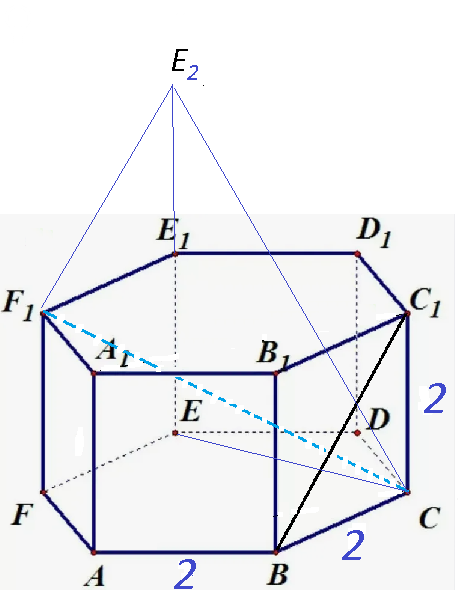
F_(1)E_(2)||FE_(1) || BC_(1)

Угол между BC_(1) и СF_(1)

равен углу между F_(1)E_(2) и СF_(1), а это ∠ СF_(1)E_(2)


EC=2sqrt(3) -меньшая диагональ шестиугольника
FC=4 - большая диагональ шестиугольника
F_(1)C=sqrt(4^2+2^2)=sqrt(20)

F_(1)E_(2)=BC_(1)=2sqrt(2)

CE^2_(2)=CE^2+EE^2_(2)=(2sqrt(3))^+4^2=12+16=28

СE_(2)=2sqrt(7)

Из треугольника СF_(1)E_(2)

CE^2_(2)=CF^2_(1)+F_(1)E^2_(2)


28=20+8

По теореме, обратной теореме Пифагора,

треугольник СF_(1)E_(2)- прямоугольный.

∠ СF_(1)E_(2)=90 °


2 способ
Ввести систему координат

c=a=2

B(1;sqrt(3);0)
C(2;0;0)
C_(1) (2;0;2)
F_(1)(-2;0;2)

vector{BC_(1)}=(2-1;0-sqrt(3);2-0)=(1;-sqrt(3);2)
vector{CF_(1)}=(2-(-2);0-0;0-2)=(4;0;-2)


Скалярное произведение векторов:
vector{BC_(1)}*vector{CF_(1)}=1*4+(sqrt(3)*0)+2*(-2)=0

vector{BC_(1)} и vector{CF_(1)} ортогональны.

Угол между ними 90 °