Задача 77076 Составить уравнение кривой второго...

6628bc203063a0176f51863a

4/24/2024 8:02:15 AM

Составить уравнение кривой второго порядка проходящей через следующие пять точек (0;0), (0;3), (6;0), (2;2), и (-2;1)

5f3eaa23faf909182968dde0

4/29/2024 7:53:10 PM

★

Уравнение кривой второго порядка имеет вид:
Ax^(2)+Bxy+Cy^(2)+Dx+Ey+F=0.
Так как кривая проходит через точку (0;0), то F=0, тогда уравнение кривой принимает вид:
Ax^(2)+Bxy+Cy^(2)+Dx+Ey=0.
Кривая проходит через точки (0;3), (6;0), (2;2), (-2;1), значит, координаты этих точек удовлетворяют уравнению кривой. Получаем систему уравнений:
{9C+3E=0,
{36A+6D=0,
{4A+4B+4C+2D+2E=0,
{4A-2B+C-2D+E=0;

{E=-3C,
{D=-6A,
{2A+2B+2C-6A-3C=0,
{4A-2B+C+12A-3C=0;

{E=-3C,
{D=-6A,
{-4A+2B-C=0,
{16A-2B-2C=0;

{E=-3C,
{D=-6A,
{C=-4A+2B,
{8A-B+4A-2B=0;

{E=-3C,
{D=-6A,
{C=-4A+2B,
{B=4A;

{E=-12A,
{D=-6A,
{C=4A,
{B=4A.

Получаем уравнение кривой:
Ax^(2)+4Axy+4Ay^(2)-6Ax-12Ay=0,
x^(2)+4xy+4y^(2)-6x-12y=0,
(x+2y)^(2)-6(x+2y)=0,
(x+2y)(x+2y-6)=0,
x+2y=0 или x+2y-6=0,
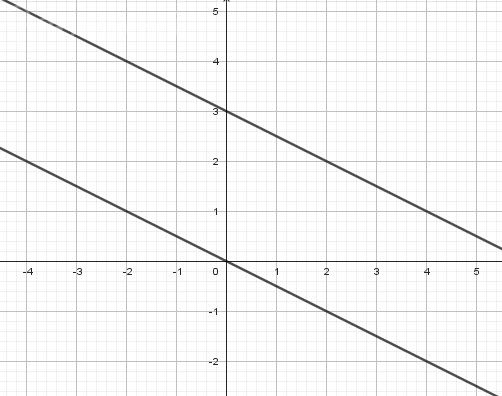
y=-(1/2)x или y=-(1/2)x+3.

Это пара параллельных прямых.