Задача 7703 Четырёхугольник ABCD с диагональю АС...

larisashakirova

12.03.2016

Четырёхугольник ABCD с диагональю АС вписан в окружность, SABCD=1/2(AB•BC+AD•DC). Докажите, что АВ^2 + ВС^2 = АС^2

SABCD=SABC+SADC. SABCD=1/2AB•BC•sin∠B+1/2AD•DCsin∠D. SABCD=1/2(AB•BC•sin∠B+AD•DCsin∠B) => sin∠B=sin∠C=1 => ∠B=∠C=90 => ∆ABC - прямоугольный. По теореме Пифагора АВ^2 + ВС^2 = АС^2, что и требовалось доказать.

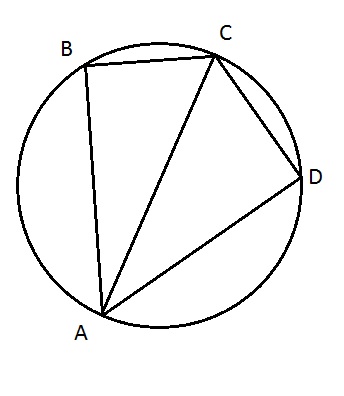
Ответ: В решение

u516520028

17.01.2017

Заданную площадь представим в виде суммы S=AB*BC/2 + AD*DC/2
Площадь четырехугольника складывается из площадей двух треугольников - АВС и АDC.
Т.к. площадь треугольника равна половине произведения основания на высоту, то из этого следует, что AB перпендикулярно ВС( SABC=AB*BC/2), а AD перпендикулярно CD (SADC=AD*CD/2). Следовательно, АВ и ВС - катеты прямоугольного треугольника АВС, а АС - его гипотенуза. Тогда, по теореме Пифагора АВ^2 + ВС^2 = АС^2, чтд.