Задача 7702 Треугольник АВС вписан в окружность, АВ...

larisashakirova

12.03.2016

Треугольник АВС вписан в окружность, АВ = 12, АС = 6, SABC = 18, угол А является острым. Найдите радиус окружности, описанной около треугольника АВС.

S∆ ABC=1/2AB•BC•sin∠A => 18=1/2•12•6•sin∠A => sin∠A=1/2 => ∠A=30. S∆=(AB•BC•AC)/(4R) => 18BC/R=18 => R=BC. Проведем высоту BH. Катет, лежащий против угла в 30 градусов, равен половине гипотенузы => BH=6. По теореме Пифагора AB^2=BH^2+AH^2, AH=√(144-36)=√108=6√3. HC=6√3-6. Из ∆CBH BC^2=BH^2+CH^2. BC^2=36+(6√3-6)^2=36+108-72√3+36=180-72√3. BC=√(180-72√3)=√(36(5-2√3))=6√(5-2√3)

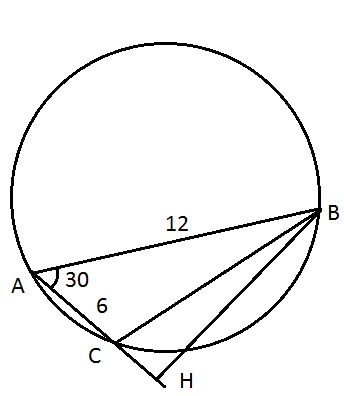
Ответ: 6√(5-2√3)