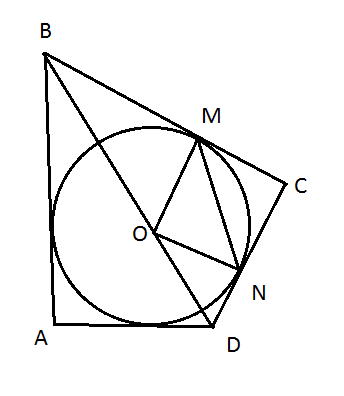
Четырёхугольник ABCD описан около окружности радиуса R. Его диагональ BD проходит через центр окружности О. Найдите MN, если М и N соответственно являются точками касания сторон ВС и DC с указанной окружностью, угол АВС = 60° и угол ADC = 120°.
математика 8-9 класс
6029
АВ и ВС касательные, проведенные из одной точки.Отрезки касательных, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Значит ∠АВD=∠CBD=30, ∠ADB=∠CDB=60 => ∠BCD=90 (180-30-60=90). ОМ⊥ВС, как радиус, проведенный в точку касания. ∠ВОМ=60 (90-30=60, по свойству острых углов прямоугольного треугольника). Аналогично, ∠NOD=30. ∠BOM+∠MOC+∠NOD=180 => ∠MOC=90. По теореме Пифагора MN^2=OM^2+ON^2. OM=ON=R => MN^2=2R^2 => MN=R√2
Ответ: R√2

