Задача 7693 Постройте эскиз графика функции. При...
Условие
system{|x^2-1|, при x меньше или равно -1; -x^2+3x+4, при x больше -1}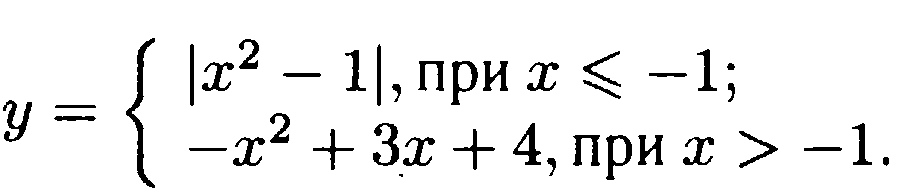
Решение
Рассмотрим функцию у=-x^2+3x+4, при x>-1. Это квадратичная функция, график парабола, ветви направлены вниз (а=-1). Вычислим координаты вершины: х0=-b/(2a)=-3/(-2)=1,5. y0=-2,25+4,5+4=6,25. Координаты вершины (1,5;6,25). Ось симметрии параболы х=1,5. График пересекает ось ОУ в точке (0;4). Найдем точки пересечения с осью ОХ. Для этого решим уравнение -x^2+3x+4=0.
D=b^2-4ac=9-4•(-1)•4=9+16=25
x1=(-b-√D)/(2a)=(-3-5)/(-2)=4
x2=(-b+√D)/(2a)=(-3+5)/(-2)=-1 - не входит в промежуток.
Построим график на заданных промежутках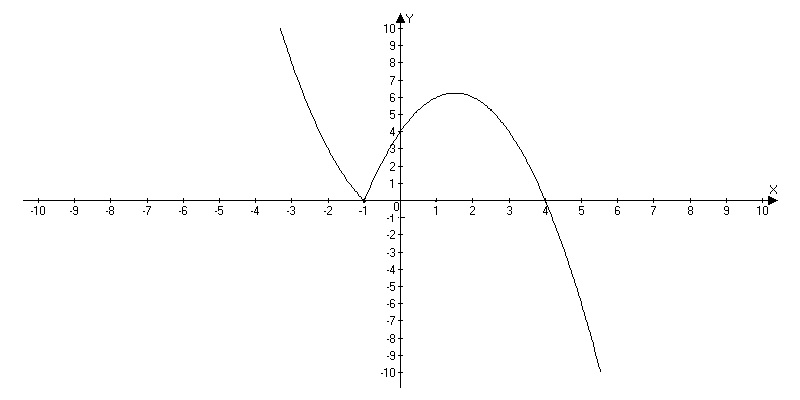
Ответ: В решение