Задача 76790 ...
Условие
3. x√(4 + y^2)dx + y√(1 + x^2)dy = 0
4. xy' - y = (x + y)ln(x + y)/y
5. xy' + (x + 1)y = 3x^2 e^-x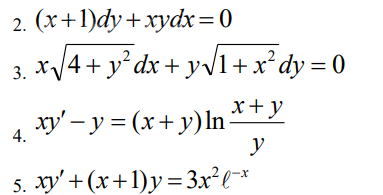
Решение
Уравнение с разделяющимися переменными
(x + 1)dy = - xydx
dy/y = -x/(x+1) dx
Берем интегралы от левой и правой части
[m]\int \frac{dy}{y} = \ln |y|[/m]
[m]\int \frac{x}{x+1} dx = \int \frac{x+1-1}{x+1} dx = \int (1 - \frac{1}{x+1}) dx = x - \ln |x+1| + \ln C = x + \ln \frac{C}{x+1}[/m]
Получаем:
[m]\ln |y| = x + \ln \frac{C}{x+1}[/m]
[m]y = e^{x + \ln \frac{C}{x+1}}[/m]
[m]y= e^{x} \cdot e^{\ln \frac{C}{x+1}}[/m]
[m]y=e^{x} \cdot \frac{C}{x+1}[/m]
3) [m]x \sqrt{4+y^2} dx + y \sqrt{4+x^2} dy= 0[/m]
Уравнение с разделяющимися переменными
[m]x \sqrt{4+y^2} dx = - y \sqrt{4+x^2} dy[/m]
[m]\frac{x}{\sqrt{4+x^2}} dx = - \frac{y}{\sqrt{4+y^2}} dy[/m]
Берем интегралы от левой и правой части
[m]\int \frac{x}{\sqrt{4+x^2}} dx[/m]
Замена 4+x^2 = t; dt = 2x dx; тогда x dx = 1/2 dt
[m]\int \frac{x}{\sqrt{4+x^2}} dx = \int \frac{dt}{2 \sqrt{t}} = \sqrt{t} = \sqrt{4+x^2}[/m]
Второй интеграл точно такой же, только с минусом:
[m]-\int \frac{y}{\sqrt{4+y^2}} dy = -\sqrt{4+y^2} + \sqrt{C}[/m]
Получаем:
[m]\sqrt{4+x^2} = -\sqrt{4+y^2} + \sqrt{C}[/m]
[m]\sqrt{4+y^2} = \sqrt{C} - \sqrt{4+x^2}[/m]
[m]4 + y^2 = (\sqrt{C} - \sqrt{4+x^2})^2 [/m]
[m]4 + y^2 = C-2\sqrt{C(4+x^2)}+4+x^2[/m]
[m]y^2 = C-2\sqrt{C(4+x^2)}+x^2[/m]
[m]y = \sqrt{C-2\sqrt{C(4+x^2)}+x^2}[/m]
4) [m]xy' - y = (x+y) \ln \frac{x+y}{y}[/m]
Делим всё уравнение на x:
[m]y' - \frac{y}{x} = \frac{x+y}{x} \cdot \ln \frac{x+y}{y}[/m]
[m]y' - \frac{y}{x} = (1+ \frac{y}{x}) \cdot \ln \frac{x+y}{y}[/m]
[m]y' = \frac{y}{x} + (1+ \frac{y}{x}) \cdot \ln \frac{x+y}{y}[/m]
[m]y' = \frac{y}{x} - (1+ \frac{y}{x}) \cdot \ln \frac{y}{x+y}[/m]
[m]y' = \frac{y}{x} - (1+ \frac{y}{x}) \cdot \ln \frac{y}{x(1+y/x)}[/m]
[m]y' = \frac{y}{x} - (1+ \frac{y}{x}) \cdot \ln \frac{y/x}{1+y/x}[/m]
Однородное уравнение 1 порядка, решается заменой:
t = y/x; y = t*x; y' = t'*x + t*x' = t'*x + t
[m]t' \cdot x + t = t - (1 + t) \cdot \ln \frac{t}{1+t}[/m]
[m]\frac{dt}{dx} \cdot x = -(1 + t) \cdot \ln \frac{t}{1+t}[/m]
Уравнение с разделяющимися переменными
[m]\frac{1}{1+t} \cdot \frac{1}{\ln \frac{t}{1+t}} dt = -\frac{dx}{x}[/m]
Интеграл от правой части табличный:
[m]-\int \frac{dx}{x} = -ln |x| - ln C = -ln |Cx|[/m]
Интеграл от левой части я не знаю, как решать.
Вольфрам Альфа показывает, что это неберущийся интеграл.
Видимо, в задании ошибка.
5) xy' + (x+1)y = 3x^2*e^(-x)
Делим всё уравнение на x:
[m]y' + \frac{x+1}{x} \cdot y = 3xe^{-x}[/m]
Неоднородное уравнение 1 порядка. Решается заменой:
y = uv; y' = u'v + uv'
[m]u'v + uv' + \frac{x+1}{x} \cdot uv = 3xe^{-x}[/m]
Выносим u за скобку:
[m]u'v + u(v' + \frac{x+1}{x} \cdot v) = 3xe^{-x}[/m]
Скобку приравниваем к 0:
[m]v' + \frac{x+1}{x} \cdot v = 0[/m]
[m]\frac{dv}{dx} = -\frac{x+1}{x} \cdot v[/m]
Уравнение с разделяющимися переменными
[m]\frac{dv}{v} = -\frac{x+1}{x} dx[/m]
Берем интегралы от обеих честей:
[m]\int \frac{dv}{v} = \ln |v|[/m]
[m]-\int \frac{x+1}{x} dx = - \int (1 + \frac{1}{x}) dx = -(x + \ln |x|)[/m]
Получаем:
[m]\ln |v| = -(x + \ln |x|)[/m]
[m]v = e^{-(x + \ln |x|)} = e^{-x} : e^{\ln |x|} = \frac{e^{-x}}{x}[/m]
Подставляем в уравнение:
[m]u'v + u(v' + \frac{x+1}{x} \cdot v) = 3xe^{-x}[/m]
[m]u' \cdot \frac{e^{-x}}{x} + u \cdot 0 = 3xe^{-x}[/m]
[m]u' \cdot \frac{e^{-x}}{x} = 3xe^{-x}[/m]
Сокращаем на e^(-x):
[m]u' \cdot \frac{1}{x} = 3x[/m]
[m]u' = 3x^2[/m]
[m]u = x^3 + C[/m]
Возвращаемся к функции y = uv:
[m]y = (x^3 + C) \frac{e^{-x}}{x}[/m]
[m]y = \frac{x^3 + C}{x} \cdot e^{-x}[/m]