Задача 76691 Найдите функцию y=f(x), для которой f '...
Условие
f ' (x) = 6x-6.
f(x) = 3x^2 - 6x + 1
f(x) = 6x^2 - 6x + 6
f(x) = 2x^3 - 6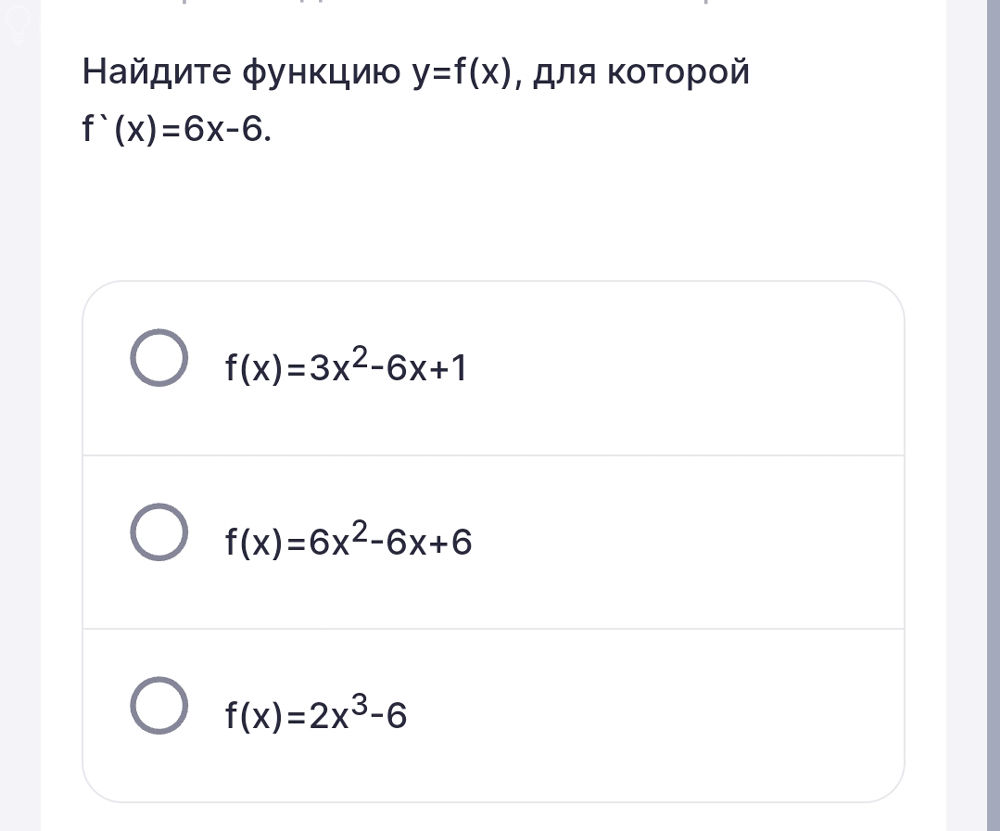
математика 10-11 класс
177
Решение
★
1) f(x)= 3x^(2)-6x+1,
f'(x)=3*2x-6+0=[b]6x-6[/b];
2) f(x)=6x^(2)-6x+6,
f'(x)=6*2x-6+0=12x-6;
3) f(x)=2x^(3)-6,
f'(x)=2*3x^(2)-0=6x^(2).
Ответ: первый вариант.