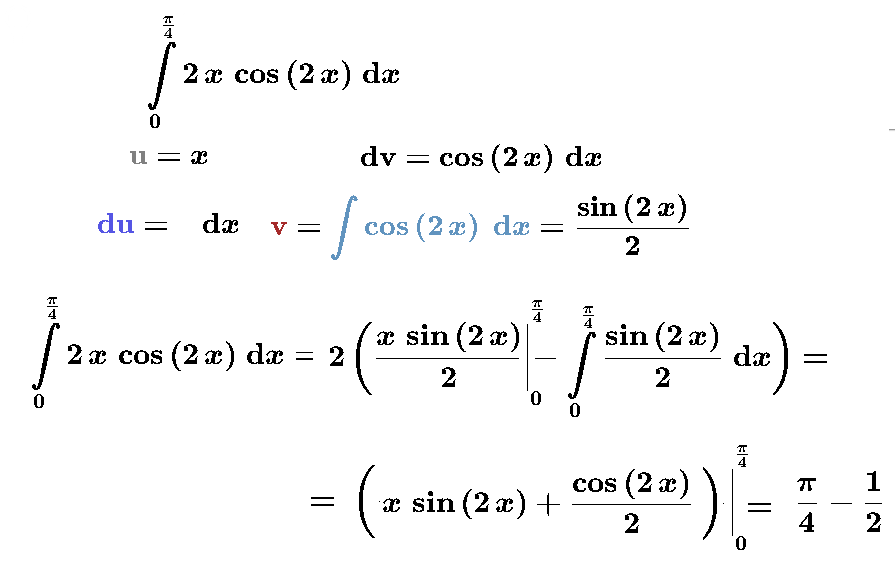Задача 76546 ...
Условие
Требуется :
1) найти плотность распределения вероятностей f(x);
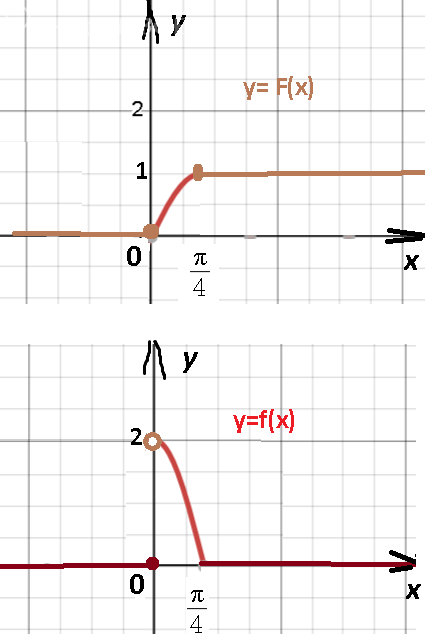
2) схематично построить графики функций f(x) и F(х);
3) найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х;
4) найти вероятность того, что Х примет значение из интервала (а;B).
Решение
Так как [m]f(x)=F `(x)[/m]
[m]f(x)=\left\{\begin{matrix}
0,если x ≤ 0\\2cos2x, если 0<x≤\frac{π}{4} \\0, если x >\frac{π}{4}\end{matrix}\right.[/m]
3)
По определению:
[m]M(X)=∫ ^{+∞ }_{- ∞ }x\cdot f(x)dx[/m]
Так как функция задана на трёх промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
[m]M(X)= ∫ ^{\frac{π}{4}}_{0}x\cdot 2cos2x dx=\frac{π}{4}-\frac{1}{2}[/m] ( см. скрин)
интегрирование по частям
По формуле:
[red]D(X)=M(X^2)-(M(X))^2[/red]
Считаем
[m]M(X^2)=∫ ^{\frac{π}{4}}_{0}x^2\cdot 2cos2x dx=\frac{π^2}{16}-\frac{1}{2}[/m]
интегрирование по частям два раза
Тогда
[m]D(X)=M(X^2)-(M(X))^2=\frac{π^2}{16}-\frac{1}{2}-(\frac{π}{4}-\frac{1}{2})^2=\frac{π}{4}-\frac{3}{4}[/m]
[red] [m]σ (X)=\sqrt{D(X)}=\sqrt{\frac{π}{4}-\frac{3}{4}}=[/m][/red]
По формуле:
[m]P( α ≤ x ≤ β )=F( β )-F( α )[/m]
получаем:
[m]P( - ∞ < x <\frac{π}{8} )=F( \frac{π}{8} )-F(- ∞ )=sin(2\cdot\frac{π}{8})-0=sin\frac{π}{4} =\frac{\sqrt{2}}{2}[/m]