Задача 76437 ...
Условие
1) tan 40° * sin 50° / sin 40° - sin 10° * cos 80°;
2) cos 24° / tan 66° - sin 24° * sin 15° / cos 75°;
3) sin a cos (90°-a) / (1 + sin² a / sin² (90°-a))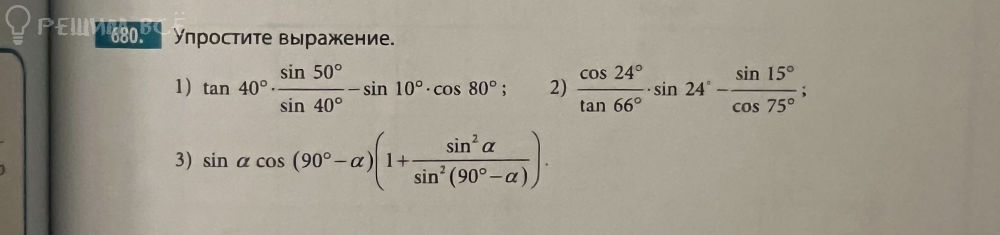
Решение
cos 80 = cos(90 - 10) = sin 10
[m]\tan 40 \cdot \frac{\cos 40}{\sin 40} - \sin 10 \cdot \sin 10 = \frac{\sin 40}{\cos 40} \cdot \frac{\cos 40}{\sin 40} - \sin^2 10 = 1-\sin^2 10 = \cos^2 10[/m]
2) tan 66 = tan(90 - 24) = ctan 24 = 1/tan 24
1/tan 66 = tan 24
cos 75 = cos(90 - 15) = sin 15
[m]\cos 24 \cdot \tan 24 \cdot \sin 24 - \frac{\sin 15}{\sin 15} = \cos 24 \cdot \frac{\sin 24}{\cos 24} \cdot \sin 24 - 1 = \sin^2 24 - 1 = - \cos^2 24[/m]
3) [m]\sin a \cdot \cos(90-a)(1 + \frac{\sin^2 a}{\sin^2(90-a)}) = \sin a \cdot \sin a (1+ \frac{\sin^2 a}{\cos^2 a}) =[/m]
[m]= \sin^2 a \cdot \frac{\cos^2 a+\sin^2 a}{\cos^2 a} = \sin^2 a \cdot \frac{1}{\cos^2 a} = \tan^2 a[/m]