Задача 76293 Найти общие и частные интегралы...
Условие
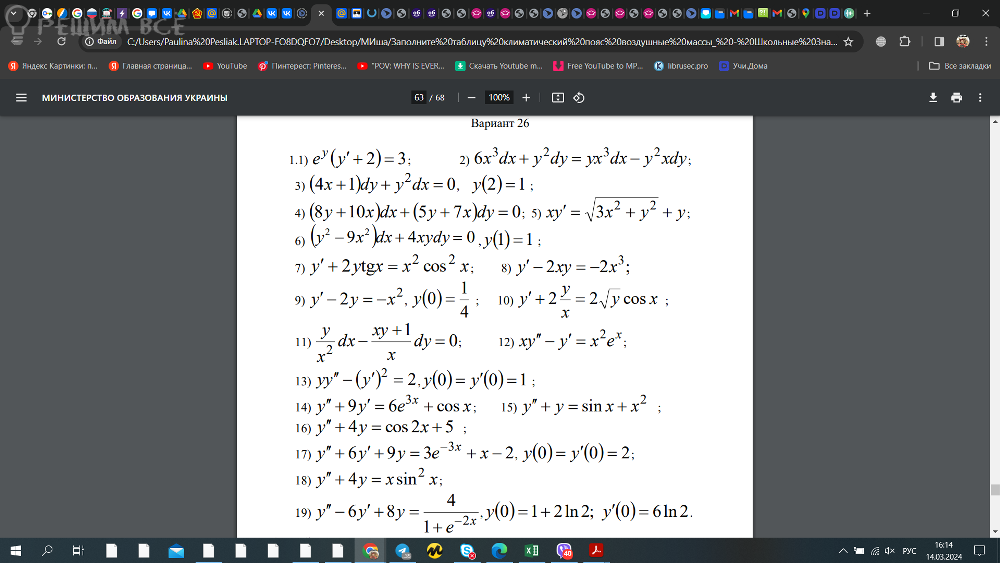
математика ВУЗ
153
Решение
★

Все решения
y`=1/x`
e^(y)*(y`+2)=3
y`+2=3*e^(-y)
y`=3*e^(-y)-2
y`=dy/dx
dy/dx=3*e^(-y)-2
dy/(3*e^(-y)-2)=dx
e^(y)dy/(3-2e^(y))=dx
Интегрируем
∫ e^(y)dy/(3-2e^(y))= ∫ dx
(-1/2) ∫ (-2e^(y))dy/(3-2e^(y))= ∫ dx
(-1/2) ∫ d(3-2e^(y))/(3-2e^(y))= ∫ dx
[b](-1/2)ln|3-2e^(y)|+C=x[/b]