Задача 76265 ...

65f181352b59d64544d7e7bd

3/13/2024 10:35:08 AM

Равнобедренный треугольник ABE находится в плоскости α. Боковые стороны треугольника ABE равны по 20 см, а сторона основания AE=32 см. К этой плоскости проведены перпендикуляр CB, который равен 6 см, и наклонные CA и CE. Вычислите расстояние от точки C до стороны треугольника AE

5f3ea7e3faf909182968ddd9

3/13/2024 7:10:34 PM

★

ВК ⊥ АЕ

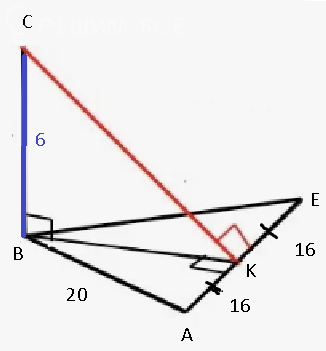
ВК- высота равнобедренного треугольника, проведенная к основанию,
а значит медиана

АК=КЕ=16

ВК^2=AB^2-AR^2=20^2-16^2=400-256=144
BK=12

Δ CBK - прямоугольный ( CB- перпендикуляр CB к плоскости α )

СK^2=CB^2+BK^2=6^2+12^2=36+144=180

CK=sqrt(180)=sqrt(36*5)=6sqrt(5)

CK ⊥ AE ( по теореме о трех перпендикулярах)

СК- искомое расстояние