Задача 7619 В правильной треугольной пирамиде SABC...
Условие
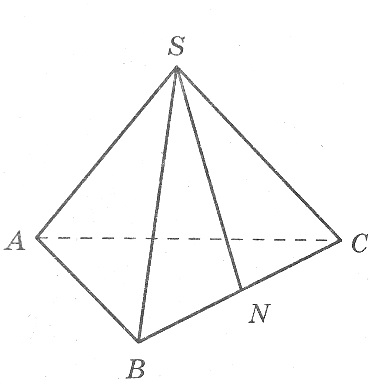
Решение
S+S+S=72
3S=72
S=24, то есть площадь треугольника BSC равна 24.
Так как треугольник BSC равнобедренный, то его медиана SN будет еще и высотой. По формуле S=1/2*a*h для поиска площади треугольника имеем:
24=1/2*BC*SN
24=1/2*BC*6
24=3*BC
BC = 8. И так как в основании правильной треугольной пирамиды правильный треугольник, то и AB=BC=8.
Ответ: 8