Задача 76179 найти все значения корня...
Условие
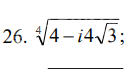
Решение
r = 8; φ = 5π/3
По формуле Муавра:
[m]x = \sqrt[4]{4 - i \cdot 4\sqrt{3}} = \sqrt[4]{8}(cos \frac{\phi + 2\pi \cdot n}{4} + i \cdot sin \frac{\phi + 2\pi \cdot n}{4})[/m]
Подставляем n = 0, 1, 2, 3, получаем:
[m]x1 = \sqrt[4]{8}(cos \frac{\phi + 2\pi \cdot 0}{4} + i \cdot sin \frac{\phi + 2\pi \cdot 0}{4}) = \sqrt[4]{8}(cos \frac{5\pi}{12} + i \cdot sin \frac{5\pi}{12})[/m]
[m]x2 = \sqrt[4]{8}(cos \frac{\phi + 2\pi \cdot 1}{4} + i \cdot sin \frac{\phi + 2\pi \cdot 1}{4}) = \sqrt[4]{8}(cos \frac{11\pi}{12} + i \cdot sin \frac{11\pi}{12})[/m]
[m]x3 = \sqrt[4]{8}(cos \frac{\phi + 2\pi \cdot 2}{4} + i \cdot sin \frac{\phi + 2\pi \cdot 2}{4}) = \sqrt[4]{8}(cos \frac{17\pi}{12} + i \cdot sin \frac{17\pi}{12})[/m]
[m]x4 = \sqrt[4]{8}(cos \frac{\phi + 2\pi \cdot 3}{4} + i \cdot sin \frac{\phi + 2\pi \cdot 3}{4}) = \sqrt[4]{8}(cos \frac{23\pi}{12} + i \cdot sin \frac{23\pi}{12})[/m]