Задача 76089 Вычислить интегралы:...
Условие
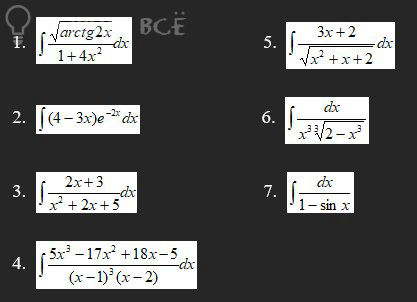
Решение
Решается заменой: arctg 2x = t; dt = 2/(1+4x^2) dx
[m]\int \frac{\sqrt{arctg(2x)}}{1+4x^2}dx = \frac{1}{2}\int \sqrt{t}dt = \frac{1}{2} \frac{t^{3/2}}{3/2} +C= \frac{1}{2} \cdot \frac{2}{3}t^{3/2}+C = \frac{1}{3}(arctg(2x))^{3/2}+C[/m]
2) [m]\int (4-3x)e^{-2x}dx[/m]
Решается по частям. u = 4 - 3x; dv = e^(-2x)dx; du = -3dx; v = -1/2*e^(-2x)
[m]\int (4-3x)e^{-2x}dx = uv - \int v du = -\frac{4-3x}{2}e^{-2x} - \frac{3}{2}\int e^{-2x} dx = -\frac{4-3x}{2}e^{-2x} + \frac{3}{4}e^{-2x} + C[/m]
3) [m]\int \frac{2x+3}{x^2+2x+5}dx = \int \frac{2x+2+1}{x^2+2x+5}dx = \int \frac{2x+2}{x^2+2x+5}dx+\int \frac{1}{x^2+2x+5}dx =[/m]
1 интеграл решается заменой: x^2 + 2x + 5 = t; dt = (2x + 2) dx
2 интеграл решается разложением знаменателя на сумму квадратов:
x^2 + 2x + 5 = x^2 + 2x + 1 + 4 = (x+1)^2 + 4
[m]= \int \frac{dt}{t} + \int \frac{1}{(x+1)^2 + 4}dx = ln |t| + \frac{1}{2}arctg(\frac{x+1}{2}) + C = ln (x^2 + 2x + 5) + \frac{1}{2}arctg(\frac{x+1}{2}) + C[/m]
4) [m]\int \frac{5x^3-17x^2+18x-5}{(x-1)^3(x-2)}[/m]
Решается методом неопределенных коэффициентов.
[m]\frac{5x^3-17x^2+18x-5}{(x-1)^3(x-2)} = \frac{A1}{x-1} + \frac{A2}{(x-1)^2} + \frac{A3}{(x-1)^3} + \frac{A4}{x-2} =[/m]
[m]= \frac{A1(x-1)^2(x-2) + A2(x-1)(x-2) + A3(x-2) + A4(x-1)^3}{(x-1)^3(x-2)} =[/m]
[m]= \frac{A1(x^2-2x+1)(x-2) + A2(x^2-x-2x+2) + A3(x-2) + A4(x^3-3x^2+3x-1)}{(x-1)^3(x-2)} =[/m]
[m]= \frac{A1(x^3-4x^2+5x-2) + A2(x^2-3x+2) + A3(x-2) + A4(x^3-3x^2+3x-1)}{(x-1)^3(x-2)} =[/m]
[m]= \frac{x^3(A1+A4) + x^2(-4A1+A2-3A4)+x(5A1-3A2+A3+3A4) + (-2A1+2A2-2A3-A4)}{(x-1)^3(x-2)} =[/m]
Составляем систему по коэффициентам при степенях x:
{ A1 + A4 = 5
{ -4A1 + A2 - 3A4 = -17
{ 5A1 - 3A2 + A3 + 3A4 = 18
{ -2A1 + 2A2 - 2A3 - A4 = -5
Решаем подстановкой:
{ A4 = 5 - A1
{ -4A1 + A2 - 3(5 - A1) = -17
{ 5A1 - 3A2 + A3 + 3(5 - A1) = 18
{ -2A1 + 2A2 - 2A3 - (5 - A1) = -5
Раскрываем скобки и Приводим подобные:
{ A4 = 5 - A1
{ -A1 + A2 = -2
{ 2A1 - 3A2 + A3 = 3
{ -A1 + 2A2 - 2A3 = 0
Снова подстановка:
{ A4 = 5 - A1
{ A2 = A1 - 2
{ 2A1 - 3(A1 - 2) + A3 = 3
{ -A1 + 2(A1 - 2) - 2A3 = 0
Раскрываем скобки и Приводим подобные:
{ A4 = 5 - A1
{ A2 = A1 - 2
{ -A1 + A3 = -3
{ A1 - 2A3 = 4
Складываем 3 и 4 уравнения:
{ A4 = 5 - A1
{ A2 = A1 - 2
{ A1 - 2A3 = 4
{ -A3 = 1
Отсюда:
{ A3 = -1
{ A1 = 4 + 2A3 = 4 + 2(-1) = 2
{ A2 = A1 - 2 = 2 - 2 = 0
{ A4 = 5 - A1 = 5 - 2 = 3
Получаем интеграл от суммы:
[m]\int (\frac{A1}{x-1} + \frac{A2}{(x-1)^2} + \frac{A3}{(x-1)^3} + \frac{A4}{x-2})dx = \int (\frac{2}{x-1} + \frac{0}{(x-1)^2} + \frac{-1}{(x-1)^3} + \frac{3}{x-2})dx =[/m]
[m]= 2ln|x-1| - \frac{(x-1)^{-2}}{-2} + 3ln|x-2| + C = 2ln|x-1| + \frac{1}{2(x-1)^2} + 3ln|x-2| + C[/m]
5, 6 и 7 выставите, пожалуйста, отдельным вопросом.
Они намного труднее, чем кажутся.