Задача 76062 (x^2-4)/log(1/2)(x^2-1) <...
Условие
log3((x+2)(x+4)) + log(1/3)(x+2) < 1/2 log(sqrt(3)) 7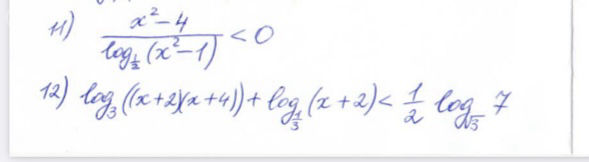
Решение
11.
Неравенство имеет смысл при
[m]\left\{\begin {matrix}x^2-1>0\\x^2-1 ≠1\end {matrix}\right.[/m] ⇒[m] (- ∞ ;-\sqrt{2})\cup(-\sqrt{2};-1) \cup(1;\sqrt{2})\cup(\sqrt{2};+ ∞ )[/m]
Решаем методом интервалов.
Нули числителя:
[m]x^2-4=0[/m]
[m]x= ± 2[/m]
___+__ (-2) __-__ ([m]-\sqrt{2}[/m]) __-__ (-1) ______+______ (1) ___-__ ( [m]\sqrt{2}[/m]) ___-___ (2) ___+__
О т в е т. (-2;-sqrt(2))U (-sqrt(2);-1)U(1;sqrt(2))U(sqrt(2);2)
12.
[m]log_{3}(x+2)(x+4)+log_{\frac{1}{3}}(x+2) < \frac{1}{2}log_{\sqrt{3}}7[/m]
Неравенство имеет смысл при
[m]\left\{\begin {matrix}(x+2)(x+4)>0\\(x+2) >0\end {matrix}\right.[/m] ⇒[m] (-2 ;+ ∞ ) [/m]
[m]log_{3}(x+2)(x+4)+log_{3^{-1}}(x+2) < \frac{1}{2}log_{3^{\frac{1}{2}}}7[/m]
[m]log_{3}(x+2)(x+4)-log_{3}(x+2) < \frac{1}{2}\cdot \frac{1}{\frac{1}{2}}log_{3}7[/m]
[m]log_{3}\frac{(x+2)(x+4)}{x+2} < log_{3}7[/m]
[m]\frac{(x+2)(x+4)}{x+2} <7[/m]
[m]x+4 <7[/m]
[m]x<3
О т в е т. (-2;-4)U(-4;3)