Задача 75988 функция у = kx+b её график проходит...

65db078658f8d021aead8679

2/25/2024 9:27:34 AM

функция у = kx+b её график проходит через точку (5;0) и касается окружности Х2 +у2 =9 Найти коэффициент к

626fab9a354ab65fb2f43abb

2/25/2024 10:23:59 AM

★

x^2 + y^2 = 9 - это окружность с центром O(0; 0) и радиусом R = 3.
Прямая y = kx + b проходит через точку (5; 0)
0 = 5k + b
b = -5k
y = kx - 5k = k(x - 5)
И эта прямая касается этой окружности
Подставим уравнение прямой в уравнение окружности:
x^2 + k^2(x - 5)^2 = 9
x^2 + k^2(x^2 - 10x + 25) - 9 = 0
(k^2 + 1)*x^2 - 10k^2*x + (25k^2 - 9) = 0
Решаем квадратное уравнение с параметром.
D/4 = (-5k^2)^2 - (k^2 + 1)(25k^2 - 9) =
= 25k^4 - 25k^4 - 25k^2 + 9k^2 + 9 = -16k^2 + 9
Так как прямая касается окружности, то они имеют 1 точку пересечения.
Это значит, что это квадратное уравнение имеет ровно 1 решение.
То есть D/4 = 0
-16k^2 + 9 = 0
k^2 = 9/16
k1 = -3/4; b1 = -5k = (-5)(-3/4) = 15/4
k2 = 3/4; b2 = -5k = (-5)(3/4) = -15/4
Получили две прямых:
y1 = -3x/4 + 15/4 = -0,75x + 3,75
y2 = 3x/4 - 15/4 = 0,75x - 3,75
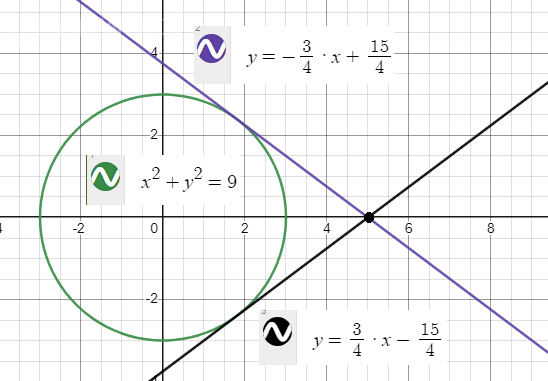
На рисунке показаны окружность и обе прямых.
Точка пересечения прямых (5; 0) тоже показана.