Задача 75956 ...

65248fdce5a6a616f313095a

2/22/2024 8:57:42 AM

Боковая сторона равнобедренного треугольника равна 9 см, а основание - 6√2 см. Найдите медиану (в см), проведенную к боковой стороне треугольника.

5f3ea7e3faf909182968ddd9

2/22/2024 9:12:31 AM

★

Находим cos ∠ B из треугольника АВС по теореме косинусов

AC^2=AB^2+BC^2-2*AB*BC*cos∠ B

(6sqrt(2))^2=9^2+9^2-2*9*9*cos ∠ B

72=81+81-162*cos ∠ B

162*cos ∠ B=81+81-72

cos ∠ B=(81+81-72)/162

cos ∠ B=[b]90/162[/b]


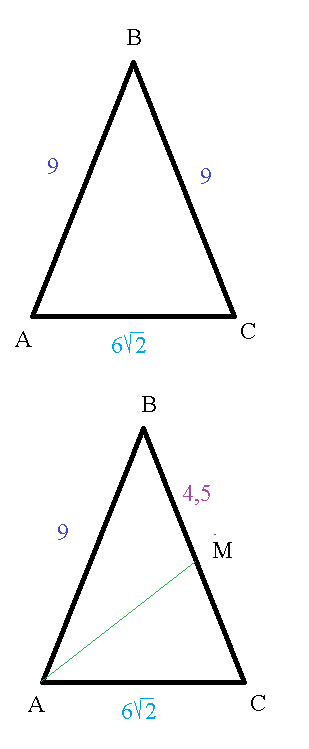
Находим медиану АМ из треугольника АВМ по теореме косинусов

AM^2=AB^2+BM^2-2*AB*BM*cos∠ B

AM^2=9^2+(4,5)^2-2*9*4,5*([b]90/162[/b])

AM^2=9^2+(4,5)^2-2*9*4,5*([b]90/162[/b])

AM^2=(360/4)

AM^2=90

[red]AM=3sqrt(10)[/red]