Задача 75901 запиши уравнение прямой ах+ву+с 0 все...
Условие
Решение
Найти: Уравнение прямой, все точки которой находятся на равном расстоянии от этих двух точек.
Решение.
Эта прямая - серединный перпендикуляр к отрезку AB.
Уравнение прямой AB через две точки:
(x - 3)/(9 - 3) = (y - 2)/(9 - 2)
(x - 3)/6 = (y - 2)/7
7(x - 3) = 6(y - 2)
7x - 21 - 6y + 12 = 0
7x - 6y - 9 = 0
Коэффициенты прямой, перпендикулярной к данной, можно найти по такой формуле:
a1*a2 + b1*b2 = 0
Где a1, a2 - коэффициенты прямых при x, b1, b2 - при y.
7*a2 - 6*b2 = 0
7*a2 = 6*b2
a2 = 6; b2 = 7
Середина отрезка AB:
M = ((3 + 9)/2; (2 + 9)/2) = (6; 5,5)
Нужная нам прямая перпендикулярна к прямой AB
7x - 6y - 9 = 0 и проходит через точку M(6; 5,5)
Уравнение прямой, перпендикулярной AB, проходящей через точку M:
6(x - 6) + 7(y - 5,5) = 0
6x - 36 + 7y - 38,5 = 0
6x + 7y - 74,5 = 0
Умножим всё уравнение на 2 и получим целые коэффициенты:
12x + 14y - 149 = 0
На рисунке видно, что все точки этой прямой действительно равноудалены от точек A и B.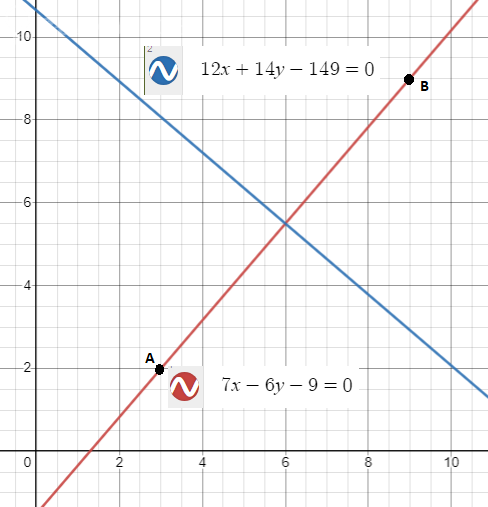
Все решения

Ответ: -7x+6y+9=0