Условие
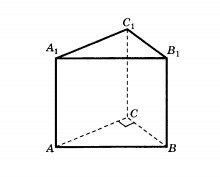
В правильной треугольной призме АВСА1В1С1, площадь основания равна 9, а боковое ребро равно 4. Найдите объём пирамиды ВАСС1А1
математика 10-11 класс
16256
Решение
Сторону треугольника примем за а. Площадь треугольника
S =(1/2)а²*sin 60°. Отсюда а = sqrt((4S) / √3). Так как S = 9, то
а = sqrt((4*9) / sqrt3) = 6 / 3^(1/4).
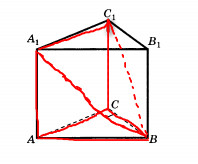
Пирамида bacc1a1 имеет в основании прямоугольник с одной стороной, равной 4, и другой, равной а.
Так как плоскость треугольника авс перпендикулярна acc1a1, то высота пирамиды - это высота правильного треугольника Н.
Н = а*sin 60° = 6 / 3^(1/4)*(sqrt3/2) = 3^(5/4).
Площадь прямоугольника S = 4a = 4*6 / 3^(1/4) = 24*3^(-1/4).
Объём пирамиды bacc1a1 V = (1/3)*S*H =
= 3^(-1)*24*3^(-1/4)*3^(5/4) = 24*3⁰ =24*1 = 24.
Ответ: 24
Вопросы к решению (5)
Жаль, что это правильная треугольная призма, в основании которой прямоугольный треугольник. Выходит он не всегда равносторонний? Или опечатались в условии задачи?
Этот прямой угол меня пугает, ладно бы ещё квадратика между углами небыло. Мне верить определению или глазам? Я не читал решения этой задачи, но тут вроде sin 60, значит верить определению.
Мы полагаем, что это равносторонний треугольник, но при этом, чтобы найти H, умножаем A на sin 60, ЧТО ТУТ ВООБЩЕ ПРОИСХОДИТ?
Каким способом была найдена высота? По формуле высоты равностороннего треугольника - другой ответ. Почему a * sin 60?
Спасибо за способ нахождения высота. Всё правильно, извините.
Все решения
Объем искомой пирамиды равен разности объемов данной призмы и объема пирамиды ВАС1В1. Объем данной призмы равен площадь основания умноженную на высоту: V=9*4=36.
Объем пирамиды ВАС1В1 равен 1/3 Sосн *ВВ1. V=1/39*4=12.
Иcкомый объем пирамиды равен 36-12=24.
Ответ: 24.
Написать комментарий



