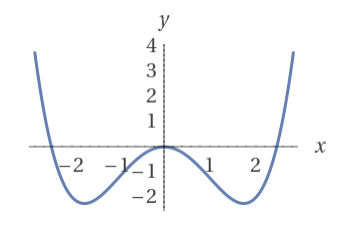
Задача 75885 Построить график функции y=1/4x^4-3/2x^2...
Условие
Решение
1. Особые точки: Находим x когда y=0, решая уравнение 1/4x^4-3/2x^2=0
Это сводится к уравнению x^4-6x^2=0, что имеет корни x = 0, x = sqrt(6), x = -sqrt(6).
2. Производная:
Вычисляем производную для нахождения минимумов и максимумов функции.
y'=x^3-3x
Снова приравниваем ее к нулю и решаем, что дает нам x = 0 и x = sqrt(3), x = -sqrt(3).
Проверив вторую производную, мы видим, что x = 0 - это максимум, а x = -sqrt(3) и x = sqrt(3) - это минимумы.
3. Построение:
Теперь, со всеми этими точками, мы можем начать строить наш график.
- Сначала рисуем оси x и y.
- Затем отметьте наши особые точки: (0,0), (sqrt(6), 0), (-sqrt(6), 0).
- Нарисуйте график функции, исходя из этих точек. Убедитесь, что у вас есть максимум на x = 0 и минимумы на x = -sqrt(3) и x = sqrt(3).