Задача 7571 ...

Julia_Trusova

09.03.2016

В ромб со стороной 10 и тупым углом (5*π)/6 вписана окружность. Определите площадь прямоугольника, вершины которого лежат в точках касания окружности со сторонами ромба.

∠BAD=∠BCD=(5*π)/6 (по условию), тогда ∠ABC=∠ADC=180-(5*π)/6=π/6
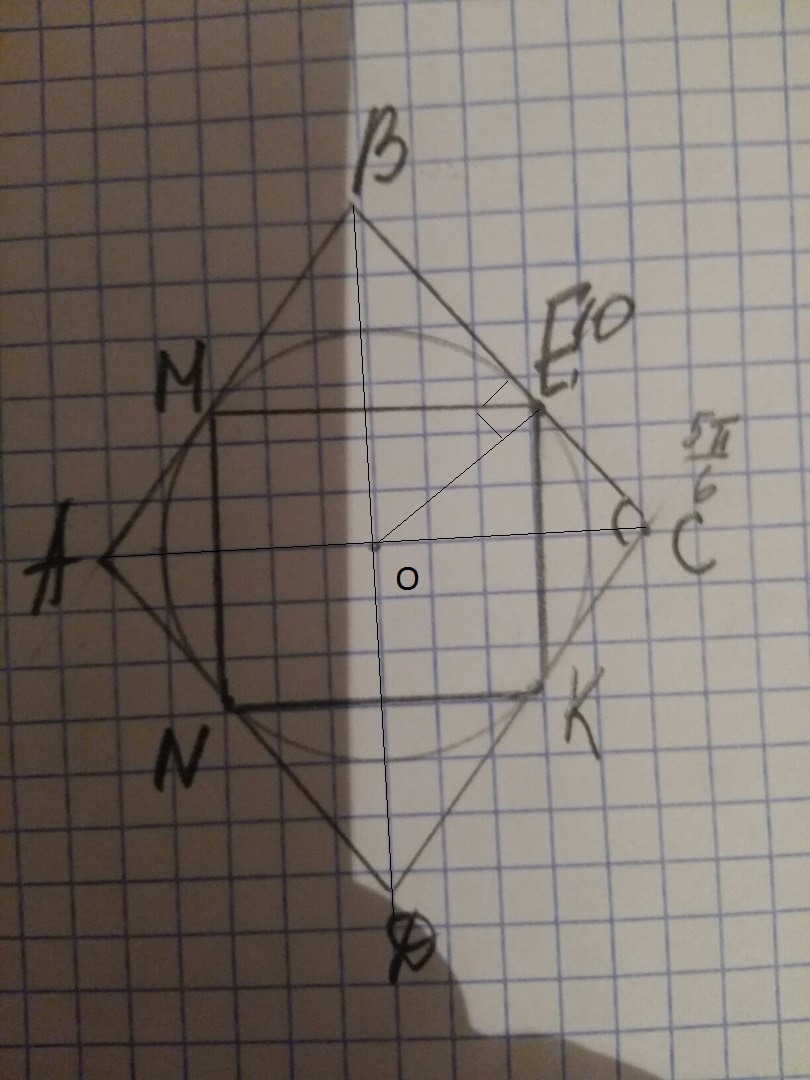
По теореме косинусов из △ABC :
AC=sqrt(10^2+10^2-2*10*10*cos(π/6))=sqrt(200-200*sqrt(3)/2)=sqrt(200*(1-sqrt(3)/2))=10*sqrt(2*(1-sqrt(3)/2))
AO=OC=AC/2=(10*sqrt(2*(1-sqrt(3)/2)))/2=5* sqrt(2*(1-sqrt(3)/2))
По теореме косинусов из △BCD :
BD=sqrt(10^2+10^2-2*10*10*cos((5*π)/6))=sqrt(200+200*sqrt(3)/2)= 10*sqrt(2*(1+sqrt(3)/2))
BO=DO=BD/2=(10*sqrt(2*(1+sqrt(3)/2)))/2=5* sqrt(2*(1+sqrt(3)/2))
Пусть EC=CK=x, тогда BE=DK=10-x ; OE=y (т.к. OE - радиус вписанной окружности, проведенный в точку касания, то OE⊥ВС)
По теореме Пифагора из △OEC:
y^2+x^2=(5*sqrt(2*(1-sqrt(3)/2)))^2
y^2=(5*sqrt(2*(1-sqrt(3)/2)))^2-x^2
y^2=50*(1-sqrt(3)/2)-x^2
По теореме Пифагора из △OEB:
y^2+(10-x)^2=(5*sqrt(2*(1+sqrt(3)/2)))^2
y^2=(5*sqrt(2*(1+sqrt(3)/2)))^2-(10-x)^2
y^2=25*2*(1+sqrt(3)/2)-(10-x)^2
Таким образом:
50*(1-sqrt(3)/2)-x^2=50*(1+sqrt(3)/2)-(10-x)^2
50-50* sqrt(3)/2-x^2-50-50* sqrt(3)/2+100-20*x+x^2=0
100-100* sqrt(3)/2=20*x
x=5-2,5*sqrt(3)
Значит, EC=CK=5-2,5*sqrt(3), BE=DK=10-(5-2,5*sqrt(3))=5+2,5*sqrt(3)
По теореме косинусов из △MBE:
ME=sqrt((5+2,5*sqrt(3))^2+(5+2,5*sqrt(3))^2-2*(5+2,5*sqrt(3))^2*cos(π/6))=sqrt(2*(5+2,5*sqrt(3))^2-2*(5+2,5*sqrt(3))^2*sqrt(3)/2))=sqrt(2*(5+2,5*sqrt(3))^2*(1-sqrt(3)/2)))
По теореме косинусов из △ECK:
EK=sqrt(2*(5-2,5*sqrt(3))^2-2*(5-2,5*sqrt(3))^2*cos((5*π)/6))=sqrt(2*(5-2,5*sqrt(3))^2*(1+sqrt(3)/2))
S(NMEK)=ME*EK= sqrt(2*(5+2,5*sqrt(3))^2*(1-sqrt(3)/2)))* sqrt(2*(5-2,5*sqrt(3))^2*(1+sqrt(3)/2))=2*(5+2,5*sqrt(3))*(5-2,5*sqrt(3))*sqrt(1-3/4)=25-6.25*3=6,25


Ответ: 6,25