Задача 75695 log2 (9-2x) =5^log5 (3-x) ...
Условие
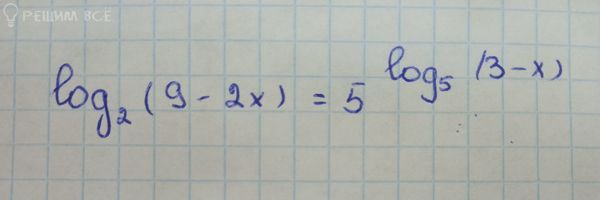
Решение
{3-x>0
{9-2x>0
{x<3
{x<4,5
Применяем основное логарифмическое тождество:
[m] 5^{log_{5}(3-x)}=3-x[/m] при 3-x >0
Уравнение принимает вид:
[b]log_(2)(9-2x)=3-x[/b]
Решается графически
См. рис.
Одна точка пересечения
x ≈ 0,247
округляем до сотых:
[b]x=0,25[/b]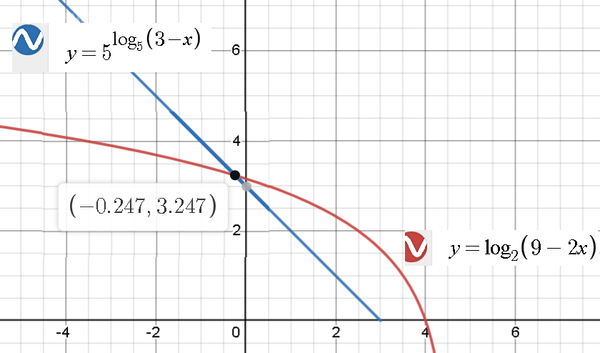
Все решения
[m]a^{log_a(b)} = b[/m]
Поэтому:
[m]log_2(9-x) = 5^{log_5(3-x)} = 3- x[/m]
Область допустимых значений для логарифма:
{ 9 - x > 0
{ 3 - x > 0
x ∈ (-oo; -3)
Опять же, по определению логарифма:
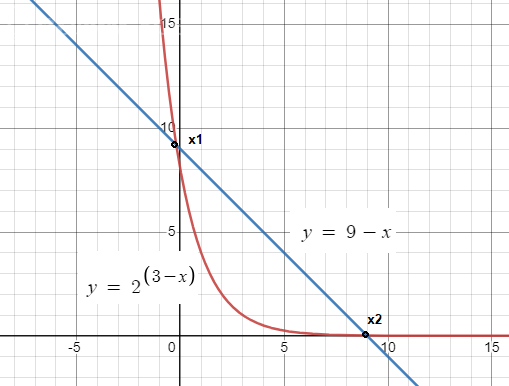
9 - x = 2^(3 - x)
Это уравнение проще всего решить графически.
Смотрите график. Кривая и прямая
x1 ≈ -0,202; y1 ≈ 9,202
x2 ≈ 8,984 > 3 - не подходит.
Ответ: x ≈ -0,202