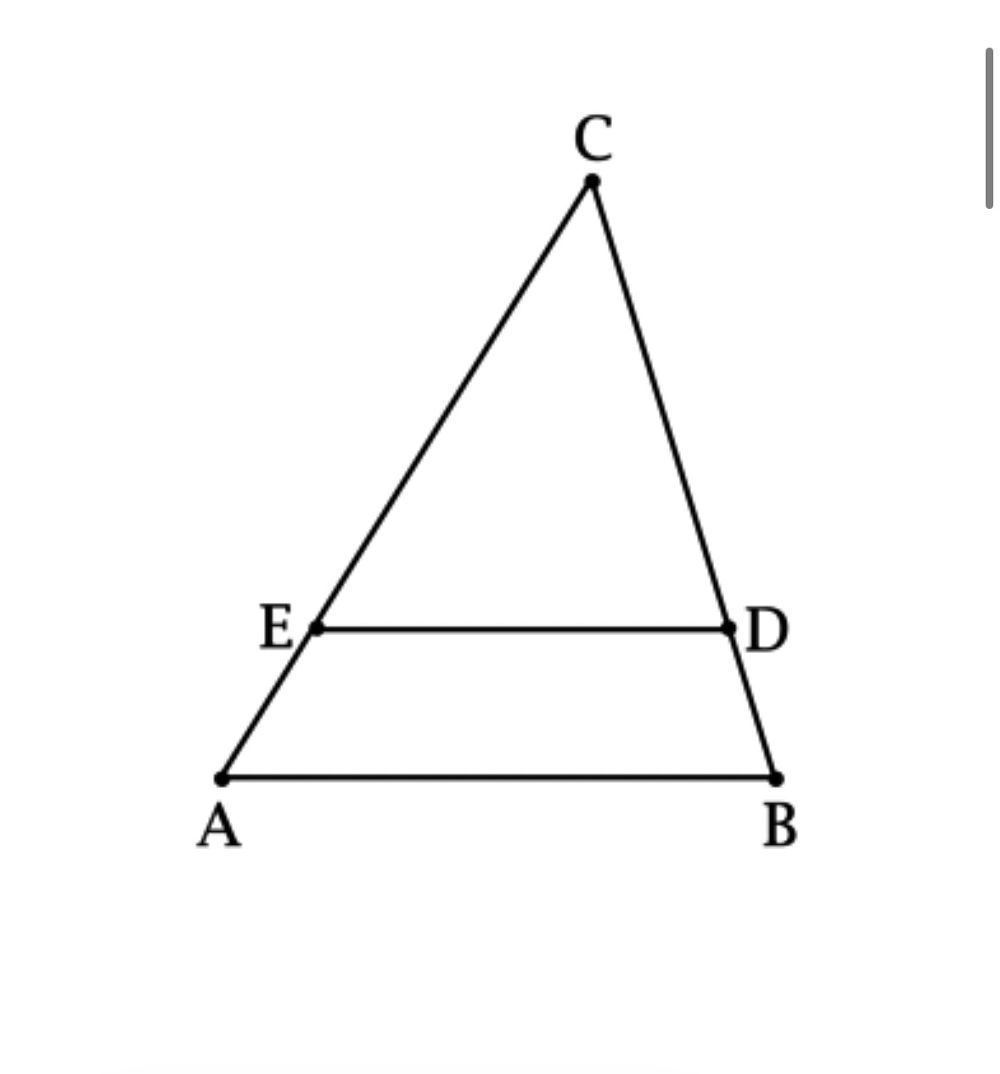
Задача 75653 Точка E лежит на стороне АС треугольника...

65bcc9a83f7efb2eafddac67

2/2/2024 10:57:08 AM

Точка E лежит на стороне АС треугольника АВС, причём ЕС/АЕ=3. Точка D лежит на ВС, причём СD/СВ=0,75. Найдите угол СЕD - угол САВ

64c75b82b635261bba022a6f

2/2/2024 11:17:31 AM

★

ΔСЕD ~ΔСАВ, по двум пропорциональным сторонам и равному углу между ними:

-∠С-общий;

-ЕС/АЕ=3/1 , те на отрезок ВС приходится 3+1=4 части и ЕС/АС=3/4;

СD/СВ=0,75=3/4 .Те 3/4=3/4.

В подобных треугольниках соответственные углы равны ⇒ ∠СЕD=∠САВ. Тогда разность равна нулю ∠СЕD - ∠САВ=0°.