Задача 75651 ...
Условие
y = 13x^2, y = 8√x.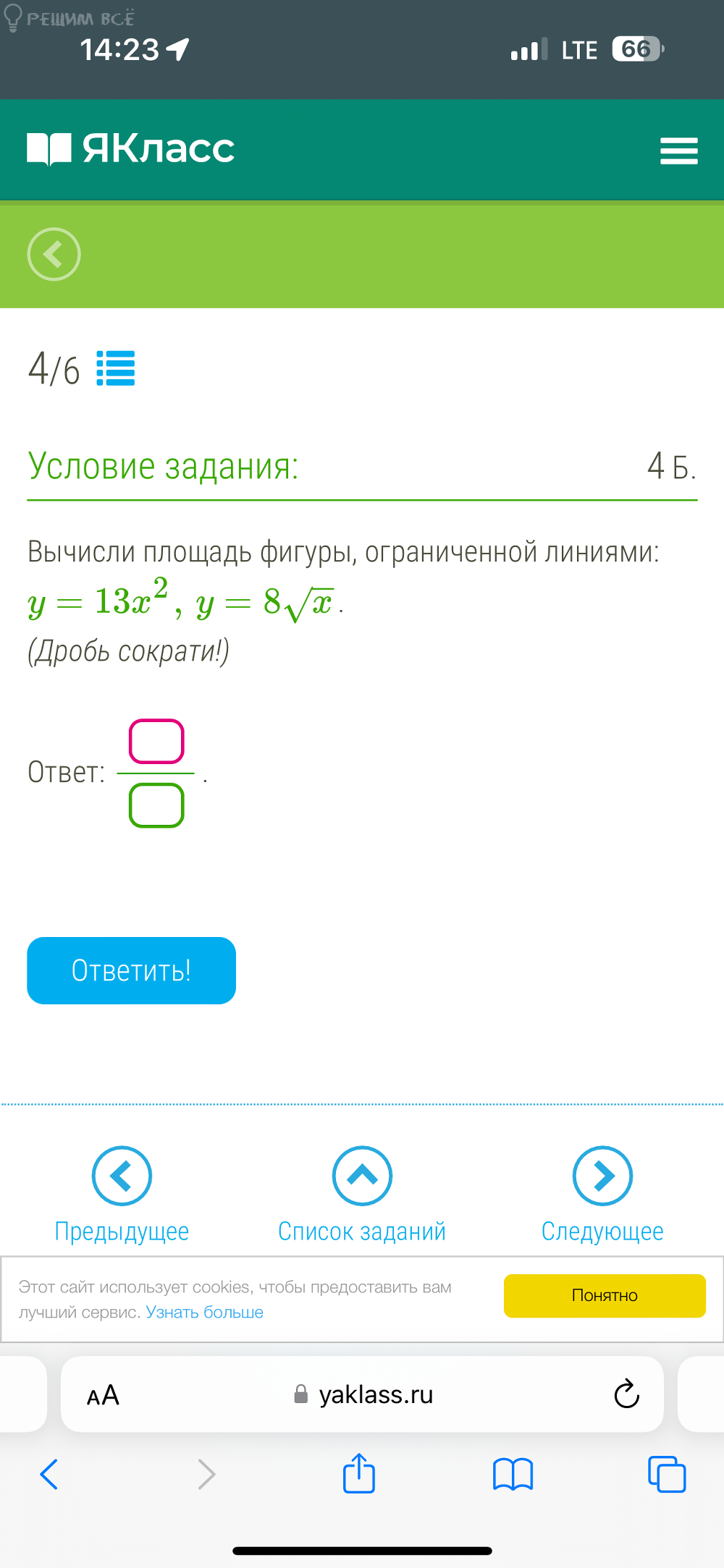
Решение
Для этого нужно приравнять функции.
13x^2 = 8sqrt(x)
13x^(3/2)*sqrt(x) - 8sqrt(x) = 0
sqrt(x)*(13x^(3/2) - 8) = 0
1) sqrt(x) = 0
x1 = 0
2) 13x^(3/2) - 8 = 0
x^(3/2) = 8/13
[m]x2 = \frac{8}{13})^{2/3}[/m]
Причем на этом промежутке кривая y=8sqrt(x) лежит выше, чем кривая y = 13x^2
[m]S = \int_0^{(\frac{8}{13})^{2/3}} (8\sqrt{x} - 13x^2) dx = \int_0^{(\frac{8}{13})^{2/3}} (8x^{1/2} - 13x^2) dx =[/m]
[m]= 8 \cdot \frac{x^{3/2}}{3/2} - 13 \cdot \frac{x^3}{3} |_0^{(\frac{8}{13})^{2/3}} = \frac{16}{3} \cdot x^{3/2} - \frac{13}{3} \cdot x^3 |_0^{(\frac{8}{13})^{2/3}} =[/m]
[m]=\frac{16}{3} \cdot ((\frac{8}{13})^{2/3})^{3/2} - \frac{13}{3} \cdot ((\frac{8}{13})^{2/3})^3 -0= \frac{16}{3} \cdot \frac{8}{13} - \frac{13}{3} \cdot (\frac{8}{13})^2 - 0 =[/m]
[m]= \frac{128}{39} - \frac{13}{3}\cdot \frac{64}{169} = \frac{128}{39} - \frac{64}{39} = \frac{64}{39}[/m]
Эта дробь не сокращается.