Задача 75646 В цилиндре площадь основания относится к...

65bbd38c3f7efb2eafddabb7

2/1/2024 5:24:21 PM

В цилиндре площадь основания относится к площади осевого сечения как п:6. Найдите угол между диагоналями осевого сечения

626fab9a354ab65fb2f43abb

2/2/2024 6:10:59 AM

★

Площадь основания цилиндра
S(осн) = π*R^2
Осевое сечение - прямоугольник, у которого длина - это диаметр цилиндра D, а высота - высота цилиндра H.
Площадь осевого сечения
S(сеч) = D*H = 2R*H
Если
S(осн) : S(сеч) = π : 6
То
π*R^2 : (2R*H) = π : 6
Отсюда
π*R : (2*H) = π : 6
2H*π = π*R*6
H = 3*R = 1,5*D
Высота осевого сечения в 1,5 раза больше основания.
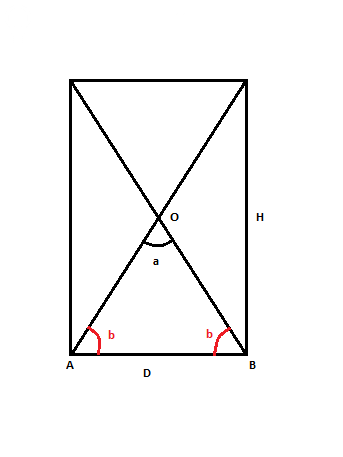
Смотрите рисунок.
Нам нужно найти угол а между диагоналями.
Нарисуем дополнительно углы b при основании.
tg b = H : D = 1,5
b ≈ 56,31°
Тогда из треугольника AOB угол
a = 180° - 2b ≈ 180° - 2*56,31° = 180° - 112,62° = 67,38°