Задача 7563 В равнобедренной трапеции диагональ...

Julia_Trusova

08.03.2016

В равнобедренной трапеции диагональ делит тупой угол пополам, большее основание меньше периметра на 25 м, а средняя линия равна 8 м. Определите длину меньшего основания трапеции.

По условию : Р-АД=25м;
средняя линия = 8м;
∠ВСА=∠АСД.
∠ВСА=∠САД как накрестлежащие при параллельных прямых АД и ВС и секущей АС
⇒ ∠АСД=∠САД и △САД - равнобедренный, ⇒ СД=АД.
Пусть АВ=АД=СД=х
Тогда Р=ВС+3*х, ⇒ ВС+3*х - х = 25,
ВС+2*х=25,
ВС=25-2*х.
Средняя линия равна полусумме оснований, т.е. средняя линия равна (ВС+х)/2=8
ВС+х=16,
ВС=16-х.
⇒25-2*х=16-х
-2*х+х=16-25
-1*х=-9
х=9
Значит, ВС=16-9=7(м)


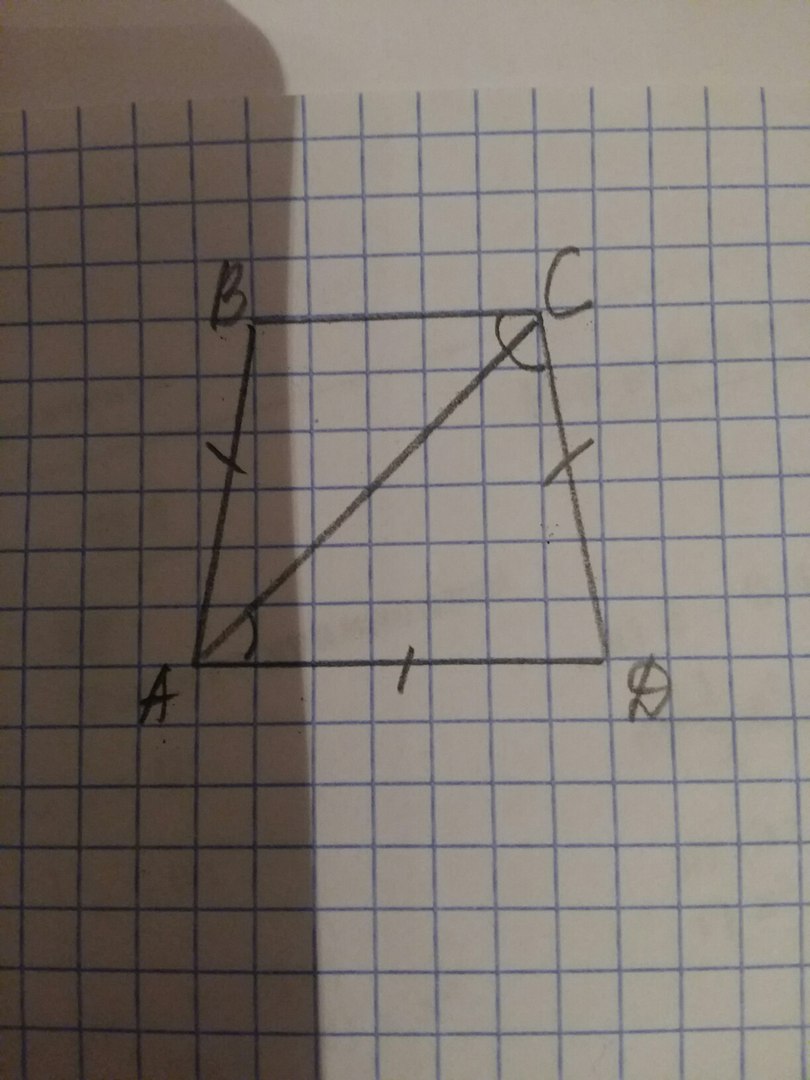
Ответ: 7