Задача 7562 Постройте график функции...

Julia_Trusova

08.03.2016

Постройте график функции у=(2x^2+3x-9)/(x+3) . Найдите значения b, при которых прямая y=b не имеет с графиком данной функции общих точек.

у=(2*х^2+3*x-9)/(x+3)
Разложим числитель 2*х^2+3*x-9 на множители, для этого приравняем его к нулю и найдем корни уравнения:
2*х^2+3*x-9=0
D=3^2-4*2*(-9)=9+72=81
x1=(-3-9)/(2*2)=-12/4=-3
x2=(-3+9)/(2*2)=6/4=1,5
Таким образом, 2*х^2+3*x-9=у=2*(х+3)(х-1,5)
Тогда функция примет вид:
у=(2*(х+3)(х-1,5))/(x+3)
ОДЗ: х+3≠0
х≠-3
у=2*(х-1,5)
y=2*x-3 - линейная функция, графиком является прямая с выколотой точкой х=-3
Построим график(график на рисунке)
При х=-3, y=-9, значит, при b=-9 прямая y=b не имеет с графиком данной функции общих точек.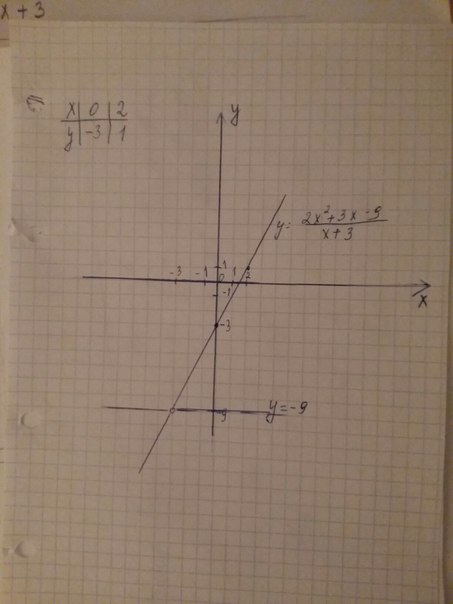

Ответ: -9