Задача 75566 решите уравнение ...
Условие
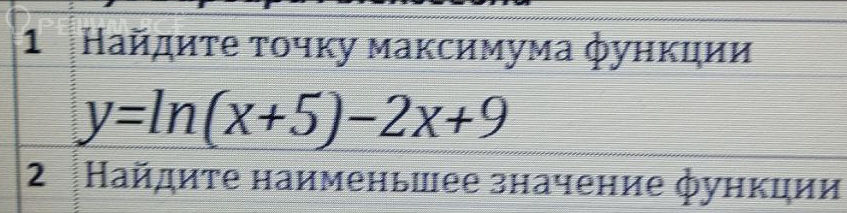
Решение
Область определения функции:
x > -5
Чтобы найти точку максимума, нужно взять производную функции и приравнять ее к 0.
[m]y' = \frac{1}{x+5} - 2 = 0[/m]
[m]\frac{1}{x+5} = 2[/m]
x + 5 = 1/2
x = 1/2 - 5 = -4,5
y(-4,5) = ln(-4,5+5) - 2(-4,5) + 9 = ln(0,5) + 18 = 18 - ln 2
Проверим, что она является точкой максимума.
При x ∈ (-5; -4,5), например, при x = -4,8, будет:
[m]y' = \frac{1}{-4,8+5} - 2 = \frac{1}{0,2} - 2 = 5 - 2 = 3 > 0[/m]
Значит, при x ∈ (-5; -4,5) функция возрастает.
При x > -4,5, например, при x = -4, будет:
[m]y' = \frac{1}{-4+5} - 2 = \frac{1}{1} - 2 = 1 - 2 = -1 < 0[/m]
Значит, при x > -4,5 функция убывает.
Таким образом, получаем: (-4,5; 18 - ln 2) - точка максимума.
Ответ: x = -4,5