Задача 75521 Задание ниже, спасибо!...
Условие
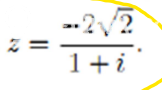
Решение
1) [m]z = \frac{-2 \sqrt{2}}{1+i} = \frac{-2 \sqrt{2}(1-i)}{(1+i)(1-i)}= \frac{-2 \sqrt{2}(1-i)}{1-i^2}=\frac{-2 \sqrt{2}(1-i)}{2} =[/m]
[m] =-\sqrt{2}(1-i) = -\sqrt{2} + \sqrt{2}i[/m]
Это алгебраическая форма.
Тригонометрическая форма:
[m]-\sqrt{2} + \sqrt{2}i = 2(-\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} \cdot i) = 2(cos \frac{3\pi}{4} + i \cdot sin \frac{3\pi}{4})[/m]
Показательная форма:
[m]2(cos \frac{3\pi}{4} + i \cdot sin \frac{3\pi}{4}) = 2e^{3\pi /4 \cdot i}[/m]
|z| = 2; arg z = 3\pi /4
2) x^3 + z = 0
x^3 = -z
[m]x^3 = \sqrt{2} - \sqrt{2}i[/m]
Переводим -z тоже в тригонометрическую форму:
[m]x^3 = 2(\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} \cdot i)[/m]
[m]x^3 = 2(cos \frac{7\pi}{4} + i \cdot sin \frac{7\pi}{4})[/m]
По формуле Муавра для корней:
[m]x = \sqrt[3]{2}(cos \frac{7\pi/4 + 2\pi \cdot n}{3} + i \cdot sin \frac{7\pi/4 + 2\pi \cdot n}{3})[/m]
x имеет 3 значения при n = 0, 1, 2:
[m]x1 = \sqrt[3]{2}(cos \frac{7\pi/4 + 2\pi \cdot 0}{3} + i \cdot sin \frac{7\pi/4 + 2\pi \cdot 0}{3}) = \sqrt[3]{2}(cos \frac{7\pi}{12} + i \cdot sin \frac{7\pi}{12})[/m]
[m]x2 = \sqrt[3]{2}(cos \frac{7\pi/4 + 2\pi \cdot 1}{3} + i \cdot sin \frac{7\pi/4 + 2\pi \cdot 1}{3}) = \sqrt[3]{2}(cos \frac{15\pi}{12} + i \cdot sin \frac{15\pi}{12})[/m]
[m]x3 = \sqrt[3]{2}(cos \frac{7\pi/4 + 2\pi \cdot 2}{3} + i \cdot sin \frac{7\pi/4 + 2\pi \cdot 2}{3}) = \sqrt[3]{2}(cos \frac{23\pi}{12} + i \cdot sin \frac{23\pi}{12})[/m]