Задача 75487 Из данной пропорции найти ...
Условие
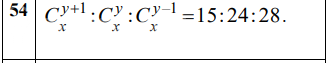

Решение
[m]C^{m}_{n} = \frac{n!}{m!(n-m)!}[/m]
Подставляем наши значения:
[m]C^{y+1}_{x} = \frac{x!}{(y+1)!(x-y-1)!}[/m]
[m]C^{y}_{x} = \frac{x!}{y!(x-y)!}[/m]
[m]C^{y-1}_{x} = \frac{x!}{(y-1)!(x-y+1)!}[/m]
По условию:
1) [m]C^{y+1}_{x} : C^{y}_{x} = 15 : 24 = 5 : 8[/m]
[m]\frac{x!}{(y+1)!(x-y-1)!} : \frac{x!}{y!(x-y)!} = 5 : 8[/m]
[m]\frac{x!}{y!(y+1)(x-y-1)!} \cdot \frac{y!(x-y-1)!(x-y)}{x!} = 5 : 8[/m]
[m]\frac{1}{(y+1)} \cdot \frac{(x-y)}{1} = 5 : 8[/m]
[m](x-y) : (y+1) = 5 : 8[/m]
[b]8(x - y) = 5(y + 1)[/b]
2) [m]C^{y}_{x} : C^{y-1}_{x} = 24 : 28 = 6 : 7[/m]
[m]\frac{x!}{y!(x-y)!} : \frac{x!}{(y-1)!(x-y+1)!} = 6 : 7[/m]
[m]\frac{x!}{(y-1)! \cdot y(x-y)!} \cdot \frac{(y-1)!(x-y)!(x-y+1)}{x!} = 6 : 7[/m]
[m]\frac{1}{y} \cdot \frac{x-y+1}{1} = 6 : 7[/m]
[m](x-y+1) : y = 6 : 7[/m]
[b]7(x - y + 1) = 6y[/b]
Получили систему двух уравнений:
{ 8(x - y) = 5(y + 1)
{ 7(x - y + 1) = 6y
Раскрываем скобки:
{ 8x - 8y = 5y + 5
{ 7x - 7y + 7 = 6y
Приводим подобные:
{ 8x - 13y = 5
{ 7x - 13y = -7
Умножаем 2 уравнение на -1:
{ 8x - 13y = 5
{ -7x + 13y = 7
Складываем уравнения:
[b]x = 12[/b]
Подставляем в любое уравнение:
8*12 - 13y = 5
96 - 5 = 13y
13y = 91
[b]y = 7[/b]
И теперь мы можем найти наше выражение:
[m]\frac{(x+3y)^2}{xy} = \frac{12 + 3 \cdot 7}{12 \cdot 7} = \frac{12 + 21}{84} = \frac{33}{84} = \frac{11}{28}[/m]