Задача 75359 Написать уравнение плоскости, ...

65a43a62925b07716243685f

1/14/2024 7:48:41 PM

Написать уравнение плоскости, проходящей через точки P и Q и перпендикулярной к заданной плоскости: p(2, 1, -1); q(4,-2, 1); 3x + 2y - 5z - 10=0

5f3ea7e3faf909182968ddd9

1/14/2024 8:22:19 PM

★

3x + 2y – 5z – 10=0- общее уравнение плоскости
значит вектор

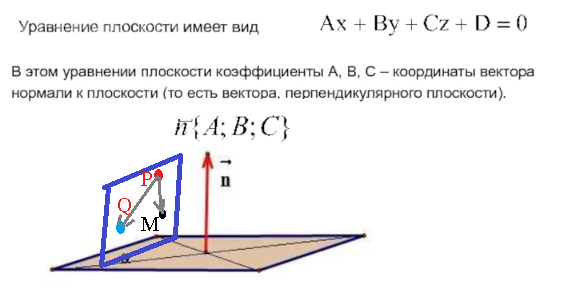
vector{n}=(3;2;-5) - нормальный вектор плоскости, который перпендикулярен ей

Плоскость перпендикулярная данной плоскости будет параллельна этому вектору


Пусть M (x;y;z) - произвольная точка искомой плоскости.

vector{PM}=(x-2;y-1;z-(-1))=(x-2;y-1;z+1)

vector{PQ}=(4-2;-2-1;1-(-1)} =(2;-3;2)

лежат в искомой плоскости.


Значит, три вектора компланарны.

Смешанное произведение равно 0


[m]\begin {vmatrix}x-2 &y-1&z+1\\2&-3&2\\3&2&-5\end {vmatrix}=0[/m]

Раскрываем определитель и получаем уравнение:


15(x-2)+6(y-1)+4(z+1)+9(z+1)-4(x-2)+10(y-1)=0

11(x-2)+16(y-1)+13(z+1)=0

[b]11x+16y+13z-25=0[/b]