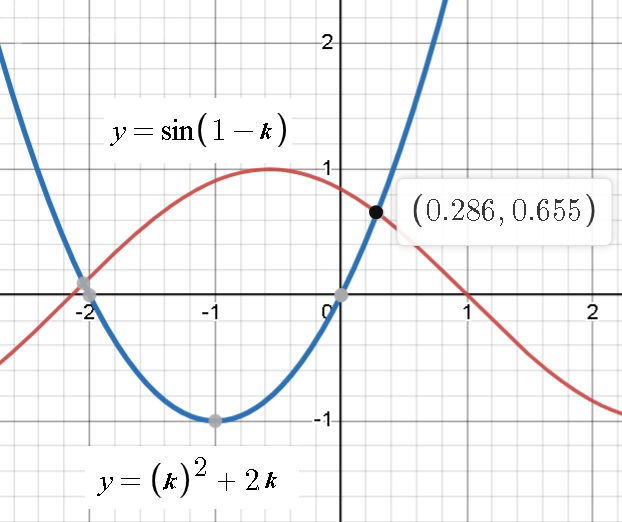Задача 75253 ...
Условие
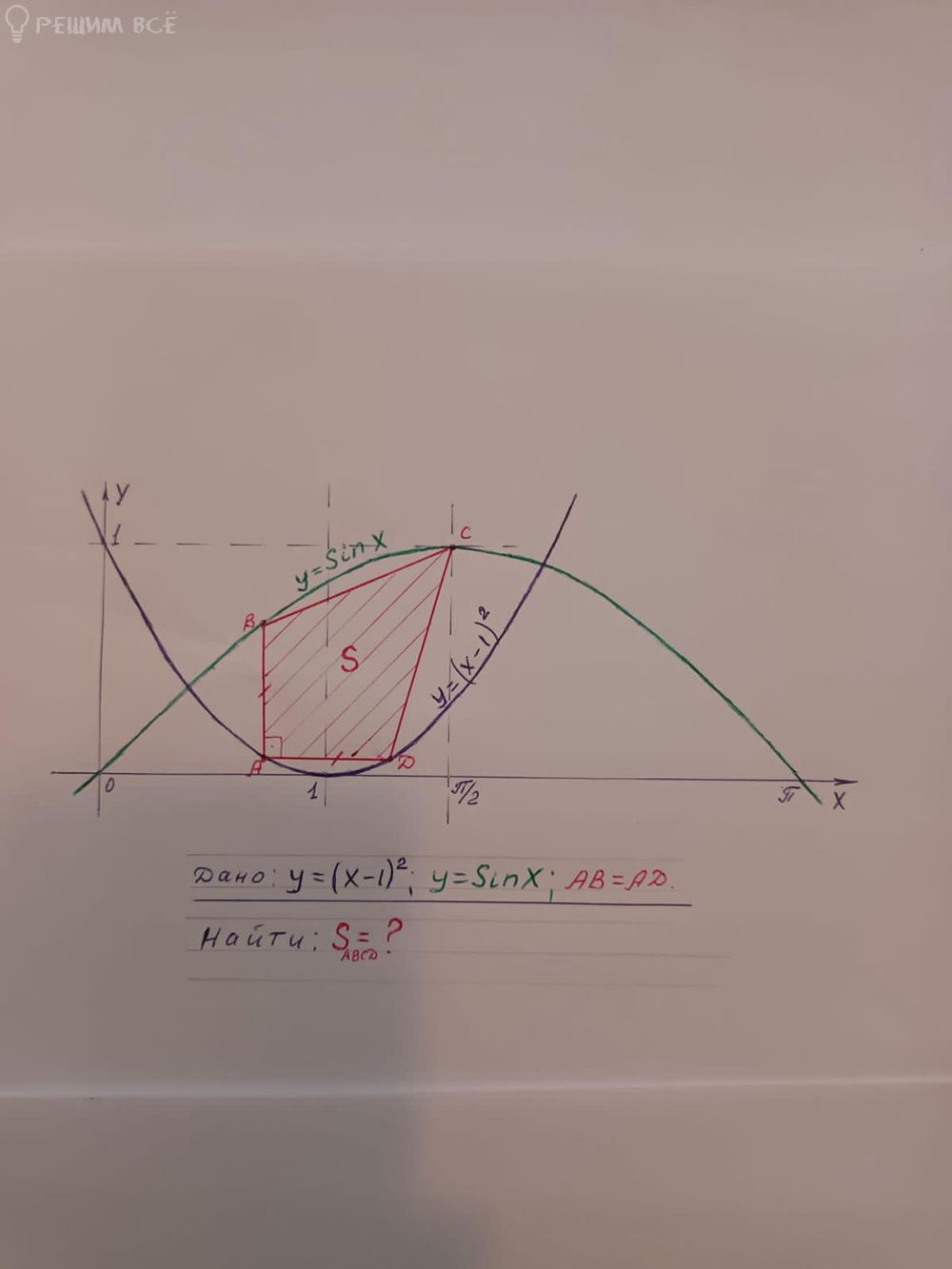
математика 8-9 класс
160
Решение
★
Значит,
x_(A)=1- k ( k >0)
x_(D)=1+k
AD=2k
y_(A)=p
y_(D)=p
x_(B)=x_(A)=1-k
y_(B)=y_(A)+AD=p+2k
Подставляем координаты точек А и D в уравнение параболы
y=(x-1)^2
p=(1-k-1)^2 ⇒ p=k^2
A(1-k; k^2)
B(1-k; k^2+2k)
D(1+k; k^2)
Точка B принадлежит кривой
y=sinx
Подставляем координаты точки В
k^2+2k=sin(1-k)
Решаем графически
k ≈ 0,286
S=S_( Δ ABD)+S_( Δ BCD)
S_( Δ ABD)=(1/2)AB*AD=(1/2)k^2=(1/2)*(0,286)^2
S_( Δ BCD)=(1/2)BC*DC*sin ∠ BCD
cos ∠ BCD найдем по теореме косинусов
BD^2=8k^2=8*(0,286)^2
BC^2=((π/2)-(1-0,286))^2+(1-0,286^2-2*0,286)^2
DC^2=((1-1-0,286))^2+(1-0,286^2)^2