Задача 75208 Нужно найти дисперсию,моду и сделать...
Условие
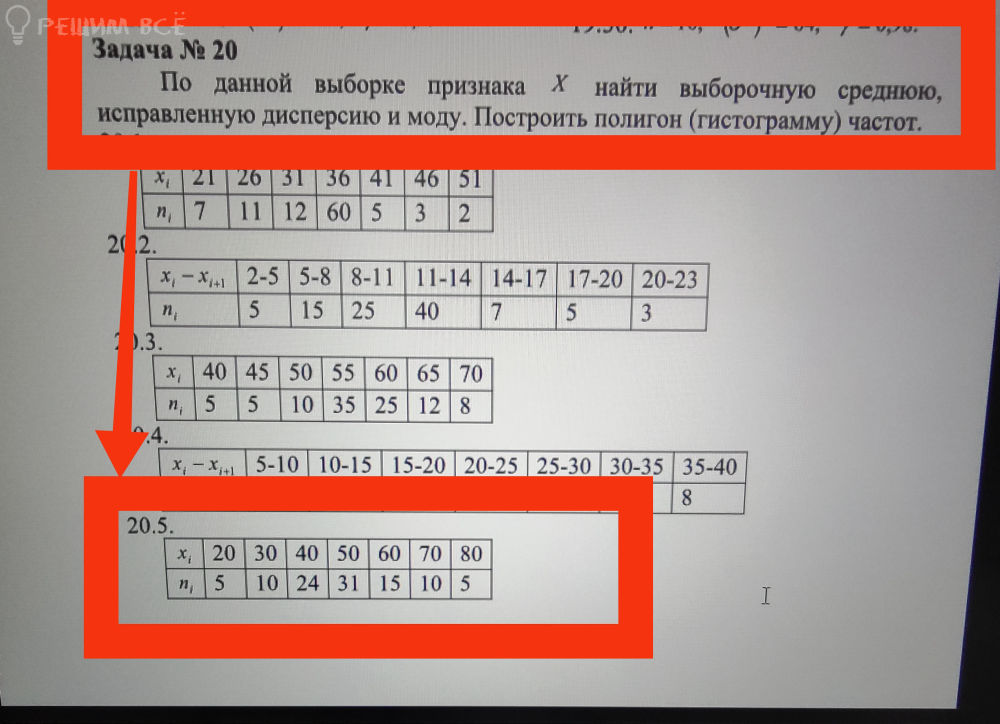
Решение
n=5+10+24+
31+15+10+5=100
Выборочная средняя находится по формуле:
[m]\overline {x_{B}}=\frac{x_{1}\cdot n_{1}+x_{2}\cdot n_{2}+x_{3}\cdot n_{3}+x_{4}\cdot n_{4}+x_{5}\cdot n_{5}+x_{6}\cdot n_{6}+x_{7}\cdot n_{7}}{n}[/m]
Подставляем значения из таблицы и считаем:
[m]\overline {x_{B}}=\frac{20\cdot 5 +30\cdot 10+40\cdot 24+50\cdot 31+60\cdot 15+70\cdot 10+80\cdot 5}{100}=[/m][b][red]?[/red][/b]
Я не считаю такое, жалко тратить время....
Для нахождения выборочной дисперсии применяем формулу, выделенную в рамочке ( см. скрин 1)
Подставляем данные из таблицы, вместо [m]\overline {x_{B}}=[/m][b][red]?[/red][/b]
и считаем:
[m] D_{B}=\frac{(20-\overline {x_{B}})^2\cdot 5+(30-\overline {x_{B}})^2\cdot 10+(40-\overline {x_{B}})^2\cdot 24+(50-\overline {x_{B}})^2\cdot 31+(60-\overline {x_{B}})^2\cdot 15+(70-\overline {x_{B}})^2\cdot 10+(80-\overline {x_{B}})^2\cdot 5}{100}=...[/m]
[b]Исправленная дисперсия [/b] ( cм. скрин 2)
[m] S^2=\frac{100}{99}\cdot ((20-\overline {x_{B}})^2\cdot 5+(30-\overline {x_{B}})^2\cdot 10+(40-\overline {x_{B}})^2\cdot 24+(50-\overline {x_{B}})^2\cdot 31+(60-\overline {x_{B}})^2\cdot 15+(70-\overline {x_{B}})^2\cdot 10+(80-\overline {x_{B}})^2\cdot 5 )=[/m]
[b]Мода:[/b]
М_(0)=50 Это значение встречается 31 раз в выборке
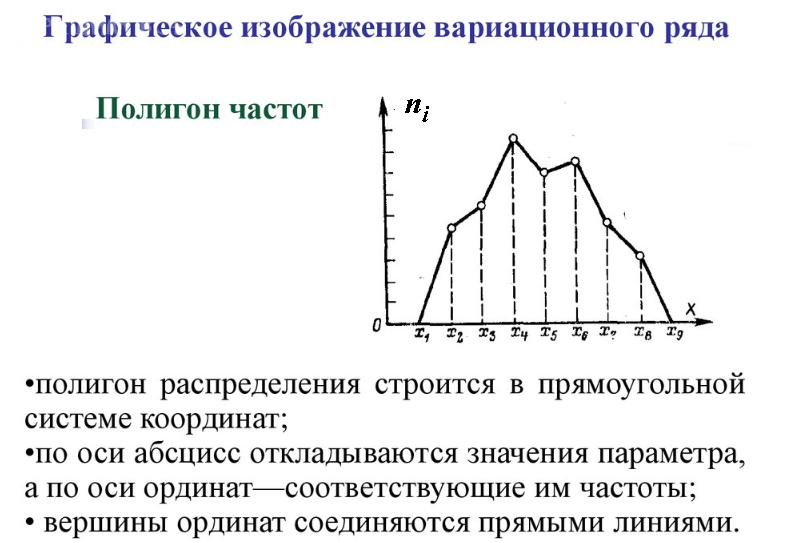
Полигон частот
Построить на координатной плоскости точки
(20;5)
(30:10)
(40;24)
(50;31)
(60;15)
(70;10)
(80;5)