Задача 75096 ...

6588522d74b9201d454ea443

12/24/2023 3:46:46 PM

решите уравнение 10^sinx=5^sinx * 2^cosx
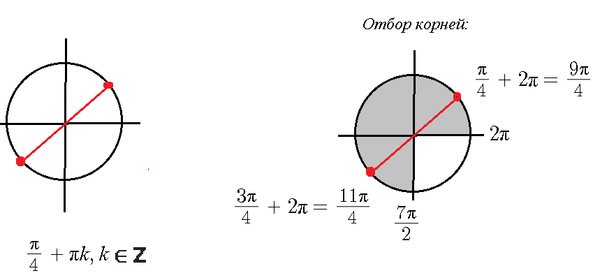
 Найдите все корни этого уравнения, принадлежащие отрезку [2pi; 7pi/2]

5f3ea7e3faf909182968ddd9

12/24/2023 3:58:55 PM

★

10=2*5


(2*5)^(sinx)=5^(sinx)*2^(cosx)

(2)^(sinx)*5^(sinx)=5^(sinx)*2^(cosx)

(2)^(sinx)*5^(sinx)-5^(sinx)*2^(cosx)=0


5^(sinx)*(2^(sinx)-2^(cosx))=0


5^(sinx) > 0 и никогда не равняется нулю


2^(sinx)-2^(cosx)=0

2^(sinx)=2^(cosx)


sinx=cosx

tgx=1

[b]x=(π/4)+πk, k ∈ Z[/b]