Задача 74593 Добрый вечер!Помогите найти значение...
Условие
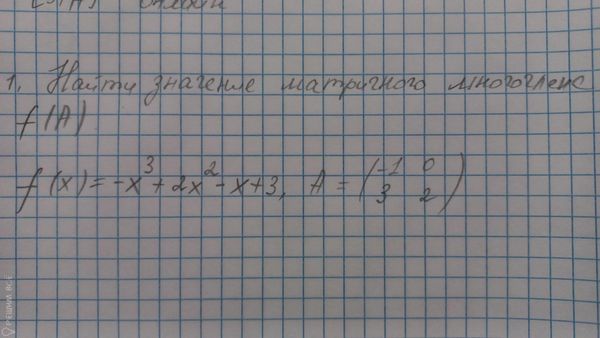
Решение
-1 & 0 \\
3 & 2 \\
\end{pmatrix}[/m]
f(x) = -x^3 + 2x^2 - x + 3
Решаем по порядку.
1) [m]A^2 = \begin{pmatrix}
-1 & 0 \\
3 & 2 \\
\end{pmatrix} \cdot \begin{pmatrix}
-1 & 0 \\
3 & 2 \\
\end{pmatrix} =[/m]
[m]\begin{pmatrix}
(-1)(-1)+0 \cdot 3 & (-1) \cdot 0+0 \cdot 2 \\
3(-1)+2 \cdot 3 & 3 \cdot 0+2 \cdot 2 \\
\end{pmatrix} = \begin{pmatrix}
1 & 0 \\
3 & 4 \\
\end{pmatrix}[/m]
2) [m]A^3= A \cdot A^2 = \begin{pmatrix}
-1 & 0 \\
3 & 2 \\
\end{pmatrix} \cdot \begin{pmatrix}
1 & 0 \\
3 & 4 \\
\end{pmatrix} = [/m]
[m]\begin{pmatrix}
(-1) \cdot 1+0 \cdot 3 & (-1) \cdot 0+0 \cdot 4 \\
3 \cdot 1+2 \cdot 3 & 3 \cdot 0+2 \cdot 4 \\
\end{pmatrix} = \begin{pmatrix}
-1 & 0 \\
9 & 8 \\
\end{pmatrix}[/m]
3) [m]3 = 3E = \begin{pmatrix}
3 & 0 \\
0 & 3 \\
\end{pmatrix}[/m]
4) Подставляем это всё и вычисляем значение:
[m]f(A)=-A^3 + 2 \cdot A^2 - A + 3E =[/m]
[m]=\begin{pmatrix}
1 & 0 \\
-9 & -8 \\
\end{pmatrix} + \begin{pmatrix}
2 & 0 \\
6 & 8 \\
\end{pmatrix} - \begin{pmatrix}
-1 & 0 \\
3 & 2 \\
\end{pmatrix} + \begin{pmatrix}
3 & 0 \\
0 & 3 \\
\end{pmatrix} =[/m]
[m]=\begin{pmatrix}
1+2-(-1)+3 & 0+0-0+0 \\
-9+6-3+0 & -8+8-2+3 \\
\end{pmatrix} = \begin{pmatrix}
7 & 0 \\
-6 & 1 \\
\end{pmatrix}[/m]