Задача 74592 По каноническому уравнению кривой...

65707c35e2fb170457c220dd

12/6/2023 3:39:42 PM

По каноническому уравнению кривой второго порядка определить тип кривой.Найти координаты фокусов ,вершин и центра . Сделать рисунок.
9х^2+5y^2+18х-30y+9=0

626fab9a354ab65fb2f43abb

12/6/2023 6:56:41 PM

★

Обожаю такие задачи!
9х^2 + 5y^2 + 18х – 30y + 9 = 0
Выделяем полные квадраты:
9(x^2 + 2x + 1 - 1) + 5(y^2 - 6y + 9 - 9) + 9 = 0
9(x + 1)^2 - 9 + 5(y - 3)^2 - 45 + 9 = 0
9(x + 1)^2 + 5(y - 3)^2 = 45
Делим всё на 45, чтобы справа была 1:
(x + 1)^2/5 + (y - 3)^2/9 = 1
Это каноническое уравнение эллипса.
Его центр A(-1; 3); полуоси a = sqrt(5); b = sqrt(9) = 3
b > a, значит, эллипс вытянут вертикально, поэтому
c^2 = b^2 - a^2 = 9 - 5 = 4
c = sqrt(4) = 2
Эксцентриситет
ε = c/b = 2/3
Фокусы будут выше и ниже центра A(-1; 3):
F1(xA; yA - c) = (-1; 3-2) = (-1; 1);
F2(xA; yA + c) = (-1; 3+2) = (-1; 5)
Вершины стоят на расстоянии b вверх и вниз от центра A(-1; 3):
B1(xA; yA - b) = (-1; 3 - 3) = (-1; 0)
B2(xA; yA + b) = (-1; 3 + 3) = (-1; 6)
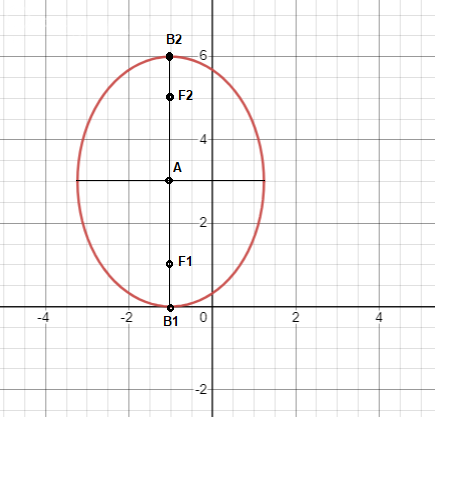
Рисунок прилагается