В трапеции ABCD биссектрисы тупых углов при основании AD пересекаются в точке Е, принадлежащей другому основанию, АЕ = 3, DE = 2,6. Найдите основания трапеции, если высота трапеции равна 2,4.
математика 8-9 класс
6555
Рассмотрим ∆AEH, где ЕН высота треугольника AED. По теореме Пифагора АН=1,8. Из ∆EHD по теореме Пифагора HD=1. AD=1,8+1=2,8. АЕ биссектриса угла BAD => ∠BAE=∠EAD=∠BEA. DE биссектриса угла ADC => ∠ADE=∠EDC=∠DEC. ∆АВЕ и ∆DEC равнобедренные. Проведем высоту ВК ∆АВЕ. ∆ВКЕ∼∆ЕНА по двум углам. => BE/AE=BK/EH=KE/AH => BE/3=1,5/1,8 => BE=2,5. Аналогично из подобия треугольников ЕМС и DHE ЕС/2,6=1,3/1 => EC=3,38. AD=2,5+3,38=5,58
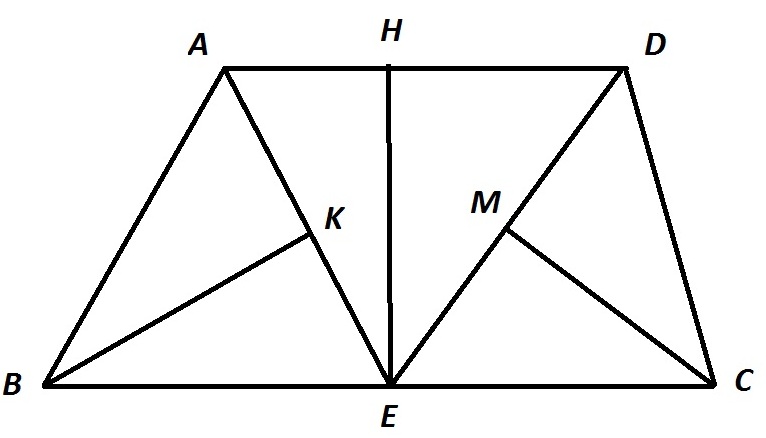
Ответ: 2,8 и 5,58

